2.3.1 Dérivation d'une fonction
Soit g(t) la dérivée de f(t). On veut exprimer G(p) en fonction de F(p).
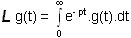On va intégrer par partie: on pose u = e-pt et g(t).dt = dv
d'où du = -p.e-pt et v = f(t) puisque g(t) est la dérivée de f(t):
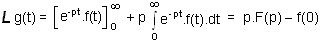
Donc dans le monde symbolique, la dérivation d'une fonction consiste à la multiplier par p et ensuite retrancher une constante correspondant à la valeur initiale de la fonction originale.
Si on extrapole le résultat précédent aux dérivées successives de f(t), on obtient:
On se rend compte que ça se complique beaucoup à cause des conditions initiales non nulles.
Ainsi, nous nous placerons toujours (aussi bien en théorie qu'en pratique) dans des conditions qui vont simplifier énormément les résultats ci-dessus.
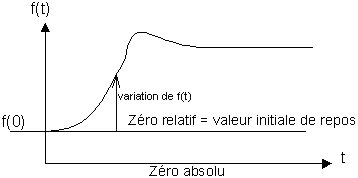Nous nous placerons toujours dans l'hypothèse suivante: le système qui va générer la fonction f(t) en réponse à une excitation d'entrée doit être initialement au repos c'est-à-dire que f(t) doit être constant avant qu'on applique un signal de commande.
Ainsi dans les expressions précédentes: f '(0) = 0 et f ''(0) = 0 et de façon générale toutes les valeurs initiales des dérivées successives de f(t) sont nulles.
Seule subsiste la valeur f(0) qui n'est pas nulle. Et bien il suffira de considérer que les fonctions du temps calculées (théorie) ou enregistrées (pratique) ne seront pas comptées à partir du zéro absolu mais seront comptées à partir de la valeur initiale de repos.
Autrement dit, ce qui nous intéresse c'est la variation de f(t) par rapport à sa valeur initiale de repos.
Exemple: si on enregistre la température de l'eau dans une casserole à partir du moment où on allume le réchaud, le zéro absolu est loin! Ce que l'on va enregistrer c'est la variation de température à partir de la valeur initiale de repos qui correspond à la température ambiante.
Il faudra toujours respecter ces conditions. Ainsi la notion de dérivation dans le monde symbolique devient un jeu d'enfant:
Le calcul de la dérivée 7ème d'une fonction du temps f(t) quelconque est très long et fastidieux. Dans le monde symbolique, il suffit de multiplier l'image de f(t) par p7.
2.3.2 Intégration d'une fonction
Nous venons de voir que, en respectant les conditions sur les valeurs initiales nulles, dans le monde symbolique la dérivation d'une fonction consiste à multiplier son image par p. Si maintenant on intègre la fonction obtenue après dérivation, on doit retrouver la fonction initiale: ainsi il faut rediviser par p donc multiplier par 1/p . Il vient:
2.3.3 Nous pouvons dès maintenant introduire la notion de Fonction de Transfert à propos du dérivateur et de l'intégrateur. Nous introduirons également la représentation d'une fonction de transfert par un graphe de transfert.
Ces notions seront reprises très en détails dans le chapitre 5, mais cela ne pose aucune difficulté de les découvrir maintenant.
On remarque que dans le monde symbolique pour exprimer la sortie d'un système, il suffit de multiplier l'entrée par la fonction de transfert du système.
La fonction de transfert du dérivateur est: Y/X = p et celle de l'intégrateur est Y/X = 1/p
2.3.4 Exemples physiques de dérivateurs et d'intégrateurs
Exemples électriques:
Prenons une self d'inductance L traversée par un courant instantané i(t).
La tension instantanée à ses bornes sera v(t) = L.di(t)/dt
En posant V(p) = L v(t) et I(p) = L i(t) on obtient: V(p) = L.pI(p) et la fonction de transfert de la self est alors V(p)/I(p) = Lp.
Prenons maintenant un condensateur de capacité C dans les mêmes conditions d'expérience. On aura v(t) = 1/C.§i(t)dt
Remarque: Le symbole § doit se lire: Somme de 0 à t (c'est une intégrale).
Donc V(p) = 1/C. I(p)/p et la fonction de transfert du condensateur est alors V(p)/I(p) = 1/Cp.
L'inductance est un dérivateur de courant et la capacité est un intégrateur de courant.
Exemples mécaniques analogues:
Prenons une masse M se déplaçant à une vitesse instantanée v(t).
La force f(t) qu'elle engendrera est proportionnelle à son accélération donc à la dérivée de sa vitesse: f(t) = M.dv(t)/dt d'où F(p) = M.pV(p) et la fonction de transfert de la masse est alors F/V = Mp.
Faisons la même expérience avec un ressort de raideur R. Cette fois la force instantanée engendrée est proportionnelle à l'élongation du ressort c.à.d. à la position instantanée de l'extrémité déplacée. La vitesse v(t) étant la dérivée de la position, la position est donc l'intégrale de la vitesse. Ainsi f(t) = R.§v(t)dt d'où F(p) = R.V(p)/p et la fonction de transfert du ressort est alors F/V = R/p.
La masse est un dérivateur de vitesse et le ressort est un intégrateur de vitesse.
Exemple hydraulique.
Prenons un récipient de section S. On le remplit avec un débit instantané q(t).
Le volume instantané contenu sera l'intégrale du débit et la hauteur de liquide h(t) est égale au volume divisé par la section du récipient: h(t) = 1/S.§q(t)dt d'où H(p) = 1/S.Q(p)/p et la fonction de transfert du récipient est alors H/Q = 1/Sp.
Le récipient est un intégrateur de débit.
Vous remarquerez l'analogie parfaite avec le condensateur.
De même en thermique nous parlons de capacité thermique. Il existe des analogies de fonctionnement dans tous les domaines de la physique. Nous reviendrons sur la mise en équations des systèmes dans le chapitre 5 (paragraphe 5.5).
