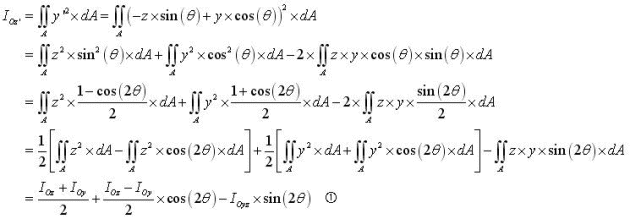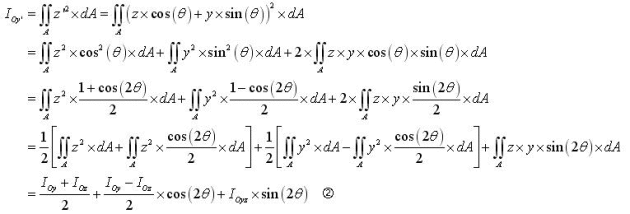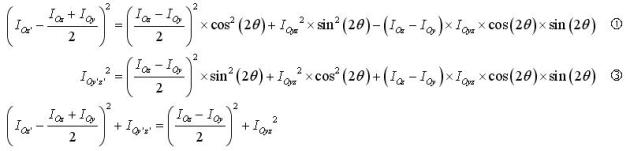Moment quadratique

Prenons une section quelconque. Les valeurs des moments quadratiques sont fonctions du repère (origine et inclinaison des axes). Observons la variation du moment quadratique pour une rotation de θ du repère (sans changer l'origine) :

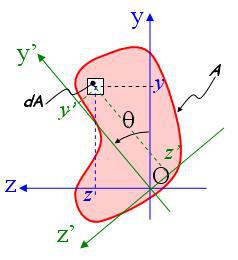
Nous savons que :

et que :

Posons :

• relations liant les coordonnées de la fibre dA dans les deux repères :

• Relations trigonométriques connues :

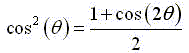
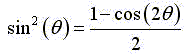
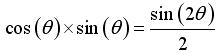
• Démonstration :

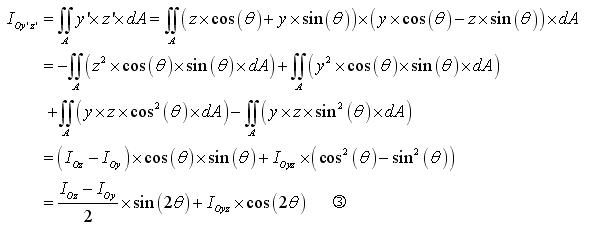
• Cercle de Mohr des moments quadratiques

Si l'on reprend les équations 1 et 3 que l'on met au carré et que l'on additionne, on a :

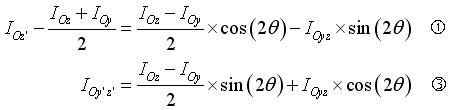
C'est l'équation d'un cercle. En effet, si on pose I_Oz ; I_Oy et I_Oyz connus, on à une équation de la forme :

de centre c d'abscisse :

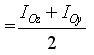
de rayon R

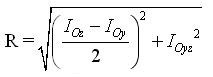
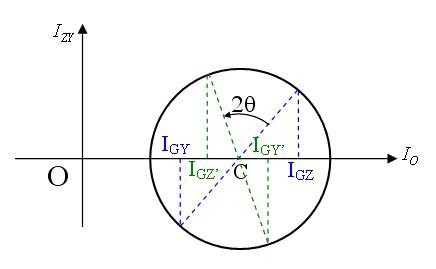
On nomme I_OZ et I_OY les extremums (moments quadratiques principaux). On a :

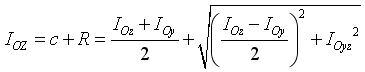
(valeur maxi) et :

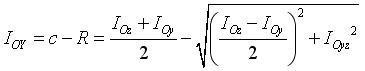
(valeur mini).

Ces deux valeurs étant éloignées de π sur le cercle, ils sont à angle droit sur la section.

Lorsque I_GZ est maximal, I_GY est minimal.