Formule de Huygens
Étudions le moment quadratique selon l'axe des y.
Cas 1 : Prenons un repère passant par le centre de gravité de la section :
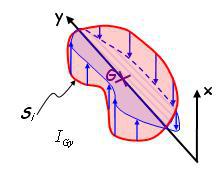
Moment quadratique selon l'axe (Gy)
Cas 2 : Et un axe parallèle quelconque :
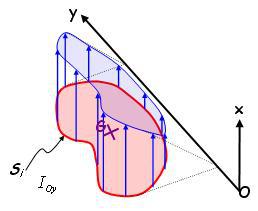
Moment quadratique selon l'axe (Oy)
En décomposant le chargement :
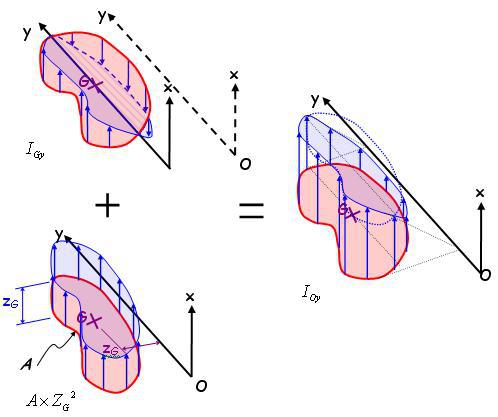
Décomposition du chargement
Nous déterminons ainsi la formule de Huygens (transposition de repères d'axes parallèles – d'un axe passant par le centre de gravité à un axe quelconque) :
Formule de Huygens : moment quadratique selon l'axe (Oy)
Le chargement a augmenté de ZG. Le moment a donc augmenté de (A x ZG) x ZG.
de même :
Formule de Huygens : moment quadratique selon l'axe (Oz)
→ Remarque : lorsqu'on réduit le chargement donnant IGy, la force résultante est nulle. Le moment est donc le même quel que soit le point de réduction – c'est pour cela que l'on s'est permis d'additionner des moments par rapport à des axes y différents.





