Quartiles
Définition :
Comme chez les séries discrètes, les quartiles
,
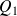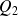et
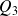d'une série continue sont 3 nombres qui découpent la série en quatre familles de même effectif.
Avec un raisonnement analogue à celui fait précédemment dans le cas de la médiane, on montre que, sous l'hypothèse de répartition uniforme des valeurs dans les classes, les quartiles
,
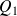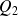et
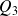correspondent approximativement aux abscisses des points d'ordonnées respectives
,
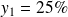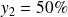et
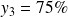du polygone des fréquences cumulées croissantes de la série classée associée à la série continue étudiée.
Exemple :
Comme chez les séries discrètes, le deuxième quartile
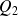d'une série continue est en fait la médiane de cette série. Or, on a vu que, dans les cas de la série
des mesures expérimentales de
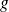, la médiane se lisait directement dans le tableau récapitulatif de la série classée associée :
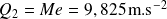
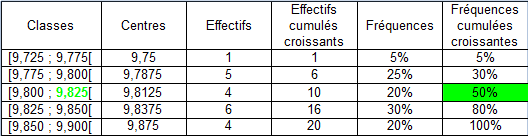
Pour ce qui est des premier et troisième quartiles, il n'en va pas de même, car la fonction fréquence cumulée croissante
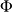ne prend pas les valeurs 25% et 75% en des limites de classes.
On remarque par contre que
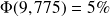et que
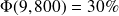. Par conséquent, le premier quartile
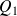qui vérifie
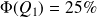est compris entre 9,775 m.s-2 et 9,800 m.s-2. En faisant l'hypothèse que les valeurs de
sont uniformément réparties dans chaque classe, la fonction
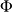est affine sur l'intervalle
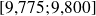et on détermine
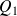par interpolation :
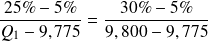
Ce qui donne :
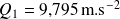
De la même façon, on détermine
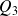dans la classe
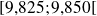, et on en déduit que 75% des mesures recueillies sont inférieures à
.
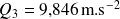