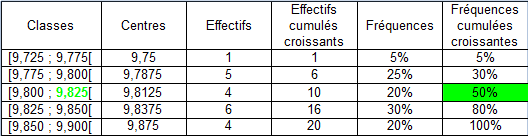
Médiane
Définition :
Comme dans le cas des séries discrètes, la médiane
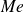 d'une série continue est un nombre qui sépare les valeurs ordonnées de la série en deux familles de même effectif. Autrement dit,
d'une série continue est un nombre qui sépare les valeurs ordonnées de la série en deux familles de même effectif. Autrement dit,
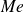 est un nombre en-dessous duquel se trouvent 50% des valeurs de la série : c'est donc le nombre associé à la fréquence cumulée croissante égale à 50%. La médiane
est un nombre en-dessous duquel se trouvent 50% des valeurs de la série : c'est donc le nombre associé à la fréquence cumulée croissante égale à 50%. La médiane
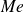 vérifie ainsi la relation :
vérifie ainsi la relation :
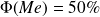
Sous l'hypothèse de répartition uniforme des valeurs dans les classes,
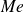 est alors l'abscisse du point d'ordonnée
est alors l'abscisse du point d'ordonnée
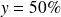 sur le polygone des fréquences cumulées croissantes de la série classée associée à la série continue étudiée.
sur le polygone des fréquences cumulées croissantes de la série classée associée à la série continue étudiée.
Finalement, si
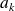 est la plus petite limite de classe telle que
est la plus petite limite de classe telle que
 , alors la médiane
, alors la médiane
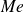 s'obtient par l'interpolation suivante :
s'obtient par l'interpolation suivante :

Exemple :
Le cas des mesures de la constante de gravitation est particulier en ce qui concerne la détermination de la médiane, car on lit dans le tableau de la série classée que :
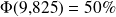
C'est-à-dire que 50% des mesures effectuées sont inférieures à 9,825 m.s-2, et donc que la médiane de la série
 est égale à cette valeur et se détermine sans calcul supplémentaire.
est égale à cette valeur et se détermine sans calcul supplémentaire.