Variance et écart-type
Définition 6
Soit X une Variable Aléatoire (VA) dont la loi est connue.
X(Ω) = {x1 ; x2 ; ... ; xn} et l'on connait p1= P(X=x1), p2= P(X=x2),..., pi= P(X=xi), ..., pn= P(X=xn), avec p1+p2+...pn=1.
La Variance de la VA X est le nombre réel noté :
V(X)= [x1-E(X)]2p1+[x2-E(X)]2p2+...+[xi-E(X)]2pi+...+[xn-E(X)]2pn, que l'on peut aussi noter :
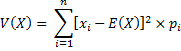
(bien que nous ayons déconseillé cette notation "X barre").
Ou encore :
Exemple 1 : la tombola
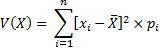
Reprenons l'exemple de la tombola dont nous rappelons la distribution ( ou loi).
| xi |
pi |
| 0 | 0,84 |
| 2 | 0,10 |
| 10 | 0,05 |
| 50 | 0,01 |
| Total | 1 |
Nous avons calculé E(X)= 1,2 €
Calculons V(X)=(0-1,2)2 x 0,84 + (2-1,2)2 x 0,10 +(10-1,2)2 x 0,05 + (50-1,2)2 x 0,01 = 28,96.
On ne sait pas trop à ce stade interpréter ce nombre : il s'exprime en euros au carré...
D'où la définition suivante : l'écart-type.
Définition 7 : l'écart-type
Soit X une Variable Aléatoire (VA) dont la loi est connue.
X(Ω) = {x1 ; x2 ; ... ; xn} et l'on connait p1= P(X=x1), p2= P(X=x2),..., pi= P(X=xi), ..., pn= P(X=xn), avec p1+p2+...pn=1.
L'écart-type de la VA X est le nombre réel noté :
Il s'exprime avec l'unité de la variable X.
Il représente une mesure de la dispersion des valeurs de la variable X autour de son espérance mathématique.
Exemple 1 : la tombola
Nous avons calculé ci-dessus V(X)= 28,96. Donc :
Le résultat s'exprime en euros. Bien que plus compréhensible immédiatemment que la variance, l'écart-type est difficilement interprétable dans l'absolu.
On pourra plus tard comparer cet écart type à une norme ou bien comparer deux écarts-types entre eux (en fait, on comparera des variances mais cela reviendra au même).