Espérance mathématique ou moyenne
Soit X une Variable Aléatoire (VA) dont la loi est connue.
X(Ω) = {x1 ; x2 ; ... ; xn} et l'on connait p1= P(X=x1), p2= P(X=x2),..., pi= P(X=xi), ..., pn= P(X=xn), avec p1+p2+...pn=1.
La Moyenne de la VA X ou Espérance mathématique de la VAX est le nombre réel noté :
E(X)= x1p1+x2p2+...+xipi+...+xnpn, que l'on peut aussi noter :
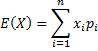
Certains auteurs utilisent aussi la notation "X barre" pour noter la moyenne de la VA X, et donc :
![]()
Cependant nous ne conseillons pas cette notation qui est source de confusion.
Reprenons l'exemple de la tombola dont nous rappelons la distribution ( ou loi).
| xi |
pi |
| 0 | 0,84 |
| 2 | 0,10 |
| 10 | 0,05 |
| 50 | 0,01 |
| Total | 1 |
Nous avons alors E(X)= 0x0,84+2x0,10+10x0,005+50x0,01=1,2.
Cela signifie que le lot moyen (qui est théorique) est d'un montant égal à 1,2 €.
Ne confondez pas le montant du lot et le gain réalisé, nous n'avons pas encore parlé du prix du billet !
Reprenons l'exemple de l'indicateur de panne dont nous rappelons la distribution (ou loi).
| xi | pi |
| 0 | 0,03 |
| 1 | O,97 |
| Total | 1 |
Nous avons alors E(X)= 0x0,03+1x0,97= 0,97.
Cela signifie que la machine est en marche en moyenne et en théorie dans 97% des cas.