A) Définition
Soit une résistance R parcourue par un courant d'intensité i(t). L'énergie dissipée par effet Joule dans la résistance est, durant le temps dt, dW = Ri².dt. Si nous voulons calculer l'énergie totale dissipée entre deux instants t1 et t2, nous devons calculer l'intégrale. Si le courant i(t) est continu de valeur Io, nous avons
W = R.Io².(t2 - t1). Un courant variable produira le même effet Joule si l'on a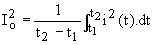 
, c'est à dire si le carré de I²o est égale à la valeur moyenne de i².
Dans tous les phénomènes thermiques interviendra donc la valeur moyenne du carré appelé, valeur quadratique moyenne ; nous utiliserons de préférence en électricité la racine de la valeur quadratique moyenne appelée valeur efficace de la fonction :
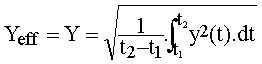
La valeur efficace se note généralement par une lettre majuscule sans indice.
Attention ! : ne pas confondre la valeur moyenne du carré et le carré de la valeur moyenne
En anglais la valeur efficace est dite RMS pour Root Mean Square soit Racine de la Moyenne du Carré ce qui précise bien l'ordre des opérations à effectuer.
B) Calcul
La valeur efficace se calcule suivant la méthode décrite au paragraphe 2.2
Calculons par exemple la valeur efficace de l'intensité de la fig.3 :
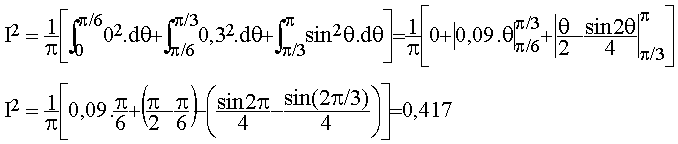
La valeur efficace du courant est donc I = 0,646 A.
C) Propriétés
P5 : soit une constante K et une fonction y(t) de valeur efficace Y, il vient :
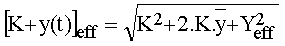
P6 : si Y = 0 alors y(t) = 0 sur tout l'intervalle
P7 :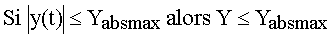 
Attention ! : calculer la valeur efficace n'est pas une opération linéaire. En particulier la valeur efficace d'une somme n'est généralement pas égale à la somme des valeurs efficaces.
