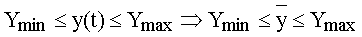A) Définition
Lorsque nous voulons charger une batterie, nous la faisons traverser d'un instant t1 à un instant t2 par un courant i(t). La charge électrique transportée par le courant est telle que : i = dq/dt. Durant le temps de charge, on a stocké dans la batterie la charge totale :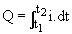 
.
Si le courant est continu, i(t) = Io = Cste et θ = (t2-t1).Io. Un courant de forme quelconque stockera la même charge si on a :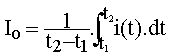 
; cette expression correspond à la somme des échantillons de la fonction i(t) divisée par l'intervalle d'étude ; elle correspond au calcul d'une moyenne.
Pour une fonction quelconque y(t), nous appellerons valeur moyenne sur l'intervalle [t1;t2] la quantité : 
Lorsque la fonction est périodique, la longueur de l'intervalle de temps est pris égal à la période :
; le résultat est indépendant de la valeur de t
o.
B) Méthode de calcul
L'intégrale définie a pour valeur l'aire algébrique limitée par le graphe de y(t), l'axe des temps et les limites d'intégration ; l'aire est comptée positivement si elle se situe au dessus de l'axe des temps (aire A1 de la fig.1) et négativement dans le cas contraire (aire A2 de la fig.1).
Lorsque cette aire a une forme géométrique simple (rectangle, triangle), il est possible de calculer la valeur moyenne sans calculer la primitive de y(t).
Etudions par exemple la tension de la fig.2 ; cette tension, affine par intervalles, est périodique avec T = 12 ms. Nous pouvons calculer l'aire limitée par le graphe :
De 0 à 3 ms, nous avons un triangle de surface
A1 = (Hauteur x Base) / 2 soit A1= 12 x 0,003 / 2 = 0,018 Vs
De 3 à 6 ms, nous avons une autre triangle de surface
A2 = 4 x 0,003 / 2 = 0,006 Vs
De 6 à 12 ms, nous avons un trapèze de surface A3 = (base 1 + base 2) x hauteur / 2 soit
A3 = ( 0,006+0,004) x10 / 2= 0,05 Vs; comme l'aire est située en dessous de l'axe des temps, l'aire algébrique sera -0,05 Vs.
La valeur moyenne de la tension est donc Vmoy = (0,018+0,006-0,05) / 0,012 = -26/12= -2,17V.
Lorsque le calcul direct de la surface n'est pas possible, il faut passer par le calcul de l'intégrale. Nous commençons par diviser l'intervalle d'étude en une suite d’intervalles [t1;t'1], [t'1;t'2] , [t'i;t'j] , [t'n;tn] tels que sur chaque intervalle la fonction y(t) ait une forme mathématique unique. Sur chaque intervalle, on doit calculer l'intégrale définie. Pour cela, il faut déterminer la primitive yp(t) de la fonction y(t) puis calculer Ini = yp(t'j)-yp(t'i). On fait ensuite la somme des intégrales pour tous les intervalles et on divise par la longueur de l'intervalle de temps.
Lorsque la fonction est périodique, le choix de l'instant to sera tel que le nombre d'intervalles soit minimum.
Nous pouvons formaliser ceci sous la forme :
Le tableau ci-dessous donne les primitives des fonctions le plus souvent rencontrées:
| Fonction | K=Cste | t | tn |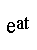 
| cos(w.t) | sin(w.t) | cos²(θ) | sin²(θ) |
| Primitive | K.t |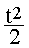 
| 
| 
| 
| 
| 
| 
|
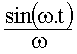
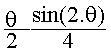
Faisons un exemple avec le courant i(t) de la fig.3.
Prenons pour variable l'angle θ = w t. La période de la fonction est alors π.
Nous découpons la période en trois intervalles:
0 < θ < π/6 : i(θ) = 0 ; ip(θ) = Cste donc A1 = 0
π/6 < θ < π/3 : i(θ) = 0,3 A et ip(θ) = 0,3.θ donc A2 = 0,3 (π/3 - π/6) = π/20
π/3 < θ < π : i(θ) = sin(θ) et ip(θ) = -cos(θ) donc A3 = -cos(π)+ cos(π/3) =1,5
Nous en déduisons la valeur moyenne : I
moy = (π/20+1,5)/ π =0,527 A.
Conseils :
lorsque la fonction contient des lignes trigonométriques (sinus, cosinus) il est préférable d'utiliser la variable
θ = w.t et d'exprimer les intervalles en angles.
Lorsque la fonction est nulle sur un intervalle, il n'est pas nécessaire de poser le calcul de l'intégrale, nous savons que le résultat sera nul sur cet intervalle.
Attention! : Lorsqu'on utilise la variable θ = w.t, les angles doivent être obligatoirement exprimées en radians.
C) Propriétés de la valeur moyenne
P1 : calculer la valeur moyenne c'est exécuter une opération linéaire :
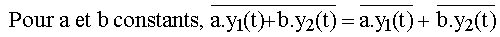
P2 : la valeur moyenne d'une fonction alternative est nulle
P3 : toute fonction périodique a une dérivée de valeur moyenne nulle
P4 : si la fonction y(t) est bornée sur l'intervalle d'étude, sa valeur moyenne a les mêmes bornes : 
