Le repliement spectral peut s'expliquer aisément de manière optique. Lorsque l'on éclaire, à l'aide d'un stroboscope dont la fréquence d'illumination est fixe, un disque en rotation ayant un marqueur sur sa périphérie, l'œil humain est capable de reconstituer le sens et la vitesse du marqueur, si la fréquence de rotation de la roue est inférieure à la moitié de la fréquence d'illumination du stroboscope. 

En revanche, si l'on augmente la vitesse de rotation au-delà de ce seuil, l'œil a l'impression que le marqueur tourne dans le sens contraire et à vitesse plus lente que la vitesse de la roue.

Le mouvement du marqueur apparaît replié.

Le repliement apparaît également lors de l'échantillonnage d'un signal, si le théorème de Shannon n'est pas respecté.(Fig. I.22)

 Théorème de Shannon:

La période d'échantillonnage Te doit être inférieure ou, dans le pire des cas, égale à la demi-période du signal échantillonné.

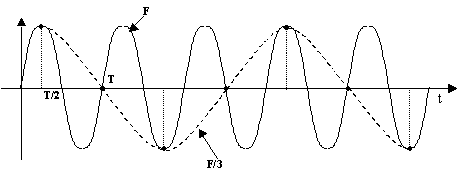
Fig. I.22  Signal sinusoïdal sous-échantillonné

avec une période d'échantillonnage Te = 3T/2

Cet échantillonnage fait apparaître un signal de fréquence F/3 qui n'est pas le reflet de la réalité.

La notion de repliement spectral est donc intimement liée au respect du théorème de Shannon.