Nous avons vu, dans l'exemple précédent, qu'un signal de fréquence F = 1GHz pulsé avec une PRF de 5kHz permettait de mesurer des phénomènes ayant des vitesses radiales:

½Vr_maxi½ £  (l/4). Fo = 375m/s

pour une distance maximale ambiguë:

d_maxi =  c/(2.Fo) = 30km

Si pour un radar de contrôle aérien cette vitesse radiale maximum semble adaptée, il en est tout autrement pour un radar météorologique. Cette vitesse est à rapprocher de la vitesse des phénomènes météorologiques mesurables. Dans les cas extrêmes, un vent de 100km/h correspond à une vitesse radiale inférieure à 20m/s,   nettement inférieure aux possibilités du système. Il suffirait donc de diminuer la PRF Fo pour diminuer la vitesse radiale maximum au profit de la distance maximum mesurable, mais cela se traduit aussi par une diminution du rapport cyclique (pour une largeur d'impulsion et une résolution radiale donnée) et donc une diminution de la portée du radar.

Une solution consiste à sommer N_c échos démodulés par une porte de distance, en supposant que le phénomène reste cohérent (vitesse constante) pendant la mesure. (Fig. I.24)

 

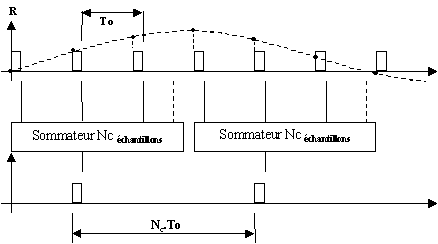
Fig. I.24   Intégration cohérente

                                                                 ½ Vr_maxi½ £  l/(4.N_c.To)

Dans notre exemple ½Vr_maxi½ £  37,5m/s avec N_c = 10

Le signal obtenu après sommation peut être traité par une FFT sur N =256 points seulement.

La résolution en vitesse dans ce cas est:

dv = 2.½Vr_maxi ½/N_m

dv = 0,3m/s

Cette méthode simple permet d'analyser des phénomènes lents en gardant une bonne portée radar, tout en ayant une résolution en vitesse acceptable et ce, en utilisant des algorithmes de FFT sur un nombre faible de points. Le phénomène observé doit cependant être cohérent pendant la durée de la mesure.

Ce temps de cohérence est de l'ordre de la millisecondes pour les radars de longueur d'onde centimétrique et de la centaine de millisecondes pour les radars de longueur d'onde métrique.

Le nombre N_c d'intégrations cohérentes existe la plupart du temps, mais il diffère en fonction du type de radar et des phénomènes que l'on veut observer. Pour un radar de contrôle aérien, le nombre minimum d'intégrations est de 4, le nombre maximum est fixé par le nombre de coups au but c'est-à-dire, le nombre d'impulsions successives touchant la cible pendant qu'elle est éclairée par le faisceau.

Exemple:

Une antenne radar 1GHz, tourne à 12tr/mn soit 0,2tr/s ou encore 72°/s, une ouverture de faisceau de 2,3° correspond à un temps de balayage d'une cible de 32ms.

Si la période de répétition des impulsions est To = 200ms, le nombre de coups au but est de 160. (Fig. I.25)

Pour N_c = 4

½Vr_maxi½ £  l/(4.N_c.To) = 337,5km/h

Si le nombre N_c d'intégration est égal à 100

½Vr_maxi½  £  13,5km/h

Ce qui est loin de couvrir le spectre des vitesses des avions

et illustre toute l'ambiguïté de la mesure Doppler !

                                        

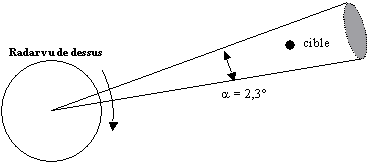
Fig. I.25   Nombre de coups au but

Est-il nécessaire de mesurer la vitesse par effet Doppler ?

La question est légitime: si le nombre de coups au but est de 100, ne peut-on pas mesurer la distance parcourue entre deux impulsions successives pour en déduire la vitesse ?

(Fig. I.26)

Pour une cible donnée se rapprochant, la distance parcourue d = c.(Tr1 – Tr2)/2 pendant l'intervalle To est représentative de la vitesse. Ceci serait possible si l'on pouvait faire la distinction entre les échos issus d'une cible mobile et ceux rétrodiffusés par une cible fixe. Cette technique, utilisée par les radars à visée laser de contrôle de vitesse automobile, est inadaptée aux  radars de contrôle aérien ou météorologiques.

L'intérêt majeur des radars Doppler est donc la possibilité de supprimer instantanément les échos à vitesse nulle.

                                     

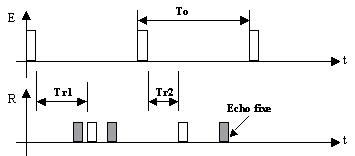
                                                           Fig. I.26  Les échos fixes