De la même façon qu'il existe
une ambiguïté sur la distance, il va apparaître une
ambiguïté relative à la mesure de vitesse de la cible.
Le signal émis est un signal
modulé en amplitude. ( Fig. I.16)
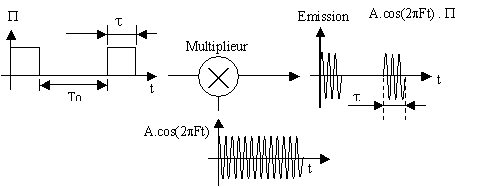
Fig.
I.16 Synoptique d'un signal
Doppler en émission
Le spectre énergétique fréquentiel du signal émis est de forme
sinx/x et est centré sur la fréquence F.
(Fig. I.17)
Spectre
discret, constitué de raies espacées de Fo
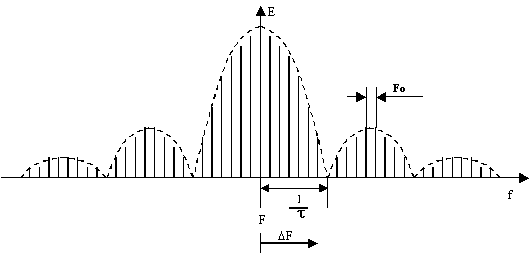
Fig.
I.17 Spectre d'un signal Doppler
Comme nous l'avons vu précédemment, une cible se rapprochant
entraîne un décalage +DF proportionnel à la vitesse, de tout le
spectre fréquentiel.
Si la
vitesse est telle que DF est égale à Fo (ou un multiple de
celle-ci), il y a coïncidence entre le spectre émis et le spectre reçu. On dit qu'il y
a repliement spectral ( aliasing ).
Tout se
passe dès lors comme si la vitesse de la cible était nulle!
Puisque l'on doit tenir compte des cibles qui s'écartent, aussi
bien que de celles qui se rapprochent, la variation de fréquence ½DF½ ne peut excéder Fo/2.
½DF½
< Fo/2
(1)
La
fréquence d'échantillonnage du signal Doppler démodulé est égale à la PRF Fo
La formule du Doppler vue précédemment nous donne quant
à elle
DF = 2.v.F/c (2)
Ces deux affirmations
imposent donc une condition sur la vitesse radiale:
(1) et (2) Þ½Vrmaxi½ £ c.Fo / 4.F = (l/4). Fo
Avec l = c/F
la longueur d'onde du signal émis
La vitesse radiale maximale mesurable, appelée vitesse de
Nyquist, est donc proportionnelle à la PRF alors que la distance maximale est, elle,
inversement proportionnelle.
Si
l'on veut mesurer des vitesses élevées, il faut choisir une PRF importante mais dans ce
cas, la distance maximale mesurable est faible.
Pour
résoudre ce dilemme, certains radars émettent plusieurs séquences d'impulsions à
plusieurs PRF différentes et sont appelés multi-PRF.
Application
numérique radar avion:
c = 3.108m/s
F=1GHz
PRF = Fo=4kHz
|Vrmaxi| = 308m/s = 1111km/h
Si l'on souhaite mesurer la
vitesse des particules solides dans les gaz, lors de l'éruption d'un volcan, la mesure de
distance s'avère moins critique, à condition évidemment de respecter une distance
minimale de sécurité, on choisira une PRF importante.
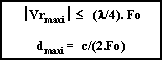
En réception, la démodulation
synchrone s'effectue par deux signaux en quadrature, une voie réelle et une voie
imaginaire, ceci pour déterminer le signe du décalage Doppler +/-
DF
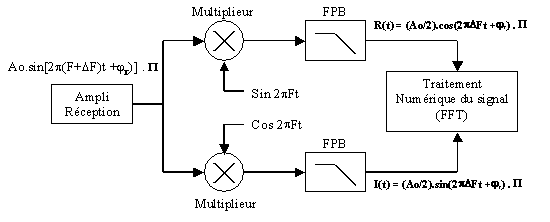
Fig. I.18 Synoptique d'un signal Doppler en réception
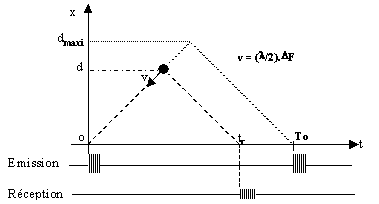
Fig. I.19 Déphasage de l'écho
Doppler
Le déphasage est fonction de la distance radiale de la cible.
d = c.tr/2
l
= c/F Þ
c = l.F
Þ
d = l.F.tr/2
Le déphasage sur la cible à la distance d est:
l
® j = 2.p
l.F.tr/2
® jd
= p/F.tr
Û jd =
2pF.d/c
jd
= 2p.d/l
Le déphasage sur le récepteur correspondant à 2d
(Si l'on néglige la variation sur l due à
l'effet Doppler)
jr
=
4p.d/l
Le signal démodulé, pour n échos issus d'une cible d'une même
porte de distance, est un signal discret,
constitué d'impulsions de largeur t à la
fréquence Fo, dont l'enveloppe est de fréquence DF . (Fig. I.20)
La largeur t étant très
faible devant la période du signal Doppler, on peut dire que le signal Doppler est
échantillonné à la période To.
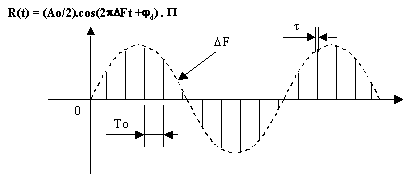
Fig. I.20 Signal reçu démodulé
P représente
l'impulsion de durée t
Ao/2
l'amplitude du signal reçu.
R(t) et I(t) sont identiques au déphasage prés.
Ce déphasage traduit le signe de DF
Le
spectre de ce signal, calculé par FFT*, (Fig. I.17)
fait apparaître (entre autres) une raie à la fréquence DF image de la
vitesse (voir annexe 4).
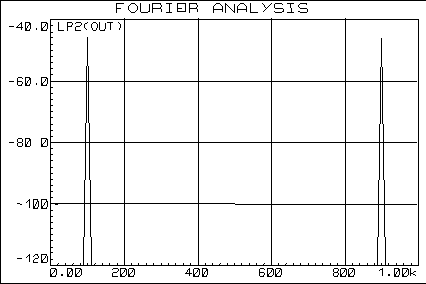
Fig. I.21 Spectre d'un signal
Doppler démodulé
*FFT (Fast Fourier Transform - Transformée de Fourier rapide) Algorithme
implanté dans un processeur de traitement du signal ou une DSP , permettant le calcul
numérique du spectre fréquentiel d'un signal échantillonné .

