A) Transformation de Laplace

1) Définition

Soit une fonction f (t) définie pour t > 0 et p un nombre complexe, la transformée de Laplace de f(t) est la fonction

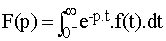
On notera aussi F (p) = L [f(t)]

 

2) Propriétés

Linéarité : L [K.f(t) + K'.g(t)] = K. L [f(t)] + K'. L [g(t)]

Retard : L [f(t-to).u(t-to)] = e^(-to.p).L [f(t).u(t)]

Dérivation : L [f '(t) ] = p. L [f(t)] - f(0^- ) ;

L [f "(t) ] = p². L [f(t)] - p.f(0^- ) - f '(0^- )

B) Transformation de Laplace inverse

1) Principe

La fonction f (t) recherchée a pour transformée de Laplace une fraction de deux polynômesà coefficients réels :

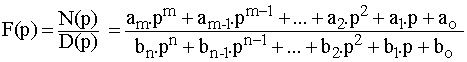avec m < n

On cherche les n racines p1, p2, ..., pn du dénominateur D(p) et on décompose F (p) en une suite de fractions élémentaires de type An/(p-pn) appelés "éléments simples"

2) Racine réelle simple

D(p) = (p-a).D'(p) avec D'(a)?0 ; dans la suite, on a l'élément simple correspondant A/(p-a) qui a pour transformée inverse ?E^(a.t)

Pour calculer le numérateur, on a A = (p-a).F(p) pour p = a

3) Racine réelle multiple

D (p) = (p-a)^k.D' (p) avec D'(a)?0 ; dans la suite, on a la série d'éléments simples correspondants :

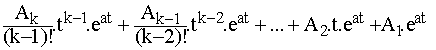
qui a pour transformée inverse

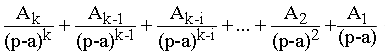
4) Racine complexe simple

D (p) a une racine complexe simple -a + j.w ; D (p) étant à coefficients réels, le nombre conjugué -a - j.w est aussi racine.

La décomposition en éléments simples de F (p) comportera les termes :

5) Calcul des numérateurs des éléments simples

Identification : réduire la série d'éléments simples au même dénominateur et identifier le numérateur obtenu à N (p), c'est à dire égaler les coefficients des termes de même degré.

Valeurs particulières : on peut calculer F (p) et la série d'éléments simples pour des valeurs particulières de p qui annulent certains termes; pour chaque valeur de p choisie, on obtient une équation contenant un certain nombre des coefficients à calculer.

C) Calcul opérationnel

1) Principe

Si le réseau étudié est initialement au repos, pour toutes les grandeurs, on a f (0^- ) = f" (0^- ) = 0. Dans ce cas, en transformée de Laplace, dériver se réduit à multiplier par p et intégrer à diviser par p.

On utilise alors un formalisme semblable à celui de la méthode complexe en régime sinusoïdal permanent :

Les valeurs complexes sont remplacées par les transformées de Laplace

L'opérateur j.w est remplacé par p

2) Impédance opérationnelle

Résistance : Z (p) = R

Inductance : Z (p) = L.p

Condensateur : Z (p) = 1/C.p

Association en série : Z (p) = SZi(p)

Association en parallèle : Y (p) = SYi(p) avec Y = 1/Z