Nous étudions des réseaux dont toutes les grandeurs sont nulles pour t < 0.

Dans ce cas, en transformée de Laplace la dérivation est équivalente à une multiplication par p

et l'intégration à une division par p.

A) Impédance opérationnelle

Soit un dipôle étudié en convention récepteur :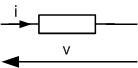

Si le dipôle est une résistance, on a v(t) = R.i(t) soit en appliquant la transformation de Laplace V(p)=R.I(p)

Si le dipôle est une inductance pure, on a v(t) = L.di(t)/dt soit en appliquant la transformation de

Laplace V(p)=L.[p.I(p) - i(0^- )] ; i étant une variable d'état et le réseau étant initialement au repos,

i(0^- ) = i(0⁺ ) = 0 donc V(p) = L.p.I(p)

Si le dipôle est un condensateur, on a i(t) = C.dv(t)/dt soit en appliquant la transformation de

Laplace I(p)=C.[p.V(p) -v(0^- )] ; v étant une variable d'état et le réseau étant initialement au repos,

v(0^- ) = v(0⁺ ) = 0 donc I(p) = C.p.V(p) ou V(p) = I(p)/C.p

On constate que pour tous les dipôles élémentaires on a une relation de la forme V(p) = Z(p).I(p) avec

Z(p) = R ou L.p ou 1.C.p.

La grandeur Z(p) est appelée impédance opérationnelle du dipôle.

La transformation de Laplace étant linéaire, les lois des noeuds et des mailles s'appliquent aux

transformées des courants et des tensions. Les lois d'association des impédances s'appliquent donc :

Pour des dipôles en série on a Zeq(p) = SZi(p)

Pour des dipôles en parallèle on a Yeq(p) = SYi(p) avec Y(p) = 1/Z(p)

Notons que l'impédance d'un circuit en régime sinusoïdal permanent devient un cas particulier

de l'impédance opérationnelle avec p = j.w

B) Calculs des réseaux

Les méthodes que l'on a utilisé en régime sinusoïdal permanent avec les valeurs efficaces et les

impédances complexes s'appliquent avec les transformées de Laplace des courants et des

tensions et les impédances opérationnelles.

On peut donc appliquer les lois de Kirchhoff et tous les théorèmes des réseaux.

Exemple 3

Étudions le dipôle représenté ci-contre :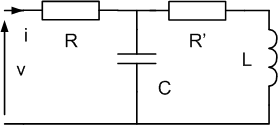

On donne e(t) = 100.t, R = 10 W , R' = 1 W , C = 1µF et L = 1 mH.

Calculons l'impédance opérationnelle du dipôle :

R' et L en série sont équivalente à l'impédance Z' = R' + L.p

Z' et C en parallèle sont équivalents à une impédance Z" :

Y" = C.p + Y' = (1+R'.C.p+L.C.p²)/(R'+L.p)

Z" et R en série sont équivalents à l'impédance Z = R + Z" soit :

Z = (R+R'+L.p+R.R'.C.p+R.L.C.p²)/ (1+R'.C.p+L.C.p²)

Cherchons le courant i(t) :

On a I(p) = V(p)/ Z(p) avec V(p) = 100/p², il vient :

I = 100.(1 + 10^-5.p+10^-8.p²)/p².(11+1,1.10^-3.p+10^-7.p²) soit

I(p) = 10⁹. (10^-8.p²+10^-5.p+1) / p².(p²+1,1.10⁴.p+11.10⁷)

Cherchons les racines du dénominateur :

p = 0 est une racine double qui donnera dans la décomposition en éléments simples les termes A/p² + B/p

Cherchons les racines de p²+1,1.10⁴.p+11.10⁷ = 0 , D' = -3,19.10^-8 < 0 donc les racines

sont complexes conjuguées -a ± j.w avec a = 5,5.10³ et w = 8,93.10³ ; ces racines donnent dans

la décomposition en éléments simples un terme de la forme [M.(p+a) +N.w ] / [(p+a)² + w²]

L'intensité est de la forme : I(p) = A/p² + B/p + [M.(p+a) +N.w ] / [(p+a)² + w²]

A = p².F(p) en p = 0 soit A = 100 /11

Pour les autres coefficients, on peut utiliser la méthode d'identification :

N(p) = 10¹⁰. (10^-8.p²+10^-5.p+1) = A.(p²+2.p.a+a²+w²) + B(p³ +2.a.p²+p.a²+p.w²)+M.(p³+p².a)+N.p².w

 

Termes en p³ : B + M = 0 ; termes en p² : A + 2.a.B+M.a+N.w = 100 ; termes en p :

2.a.A +B.(a²+.w²) = 10⁵

termes constants : A.(a²+.w²) = 10¹⁰

On en déduit : A = 100 / 11 , B = 0 , M = 0 et N = 0,01018

La fonction i(t) cherchée est donc : i(t) = 100.t/11 + 0,1018.e^(-a.t). sin(w.t)

Exemple 4

Étudions le circuit ci-dessous avec R = 1 kW et C = 1nF :

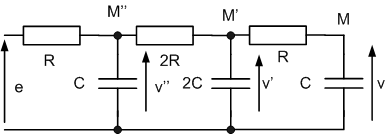
Cherchons d'abord la fonction de transfert opérationnelle T(p) = V(p) / E(p).

Pour ce type de réseau en échelle, on facilite le calcul en appliquant le théorème de Millmann :

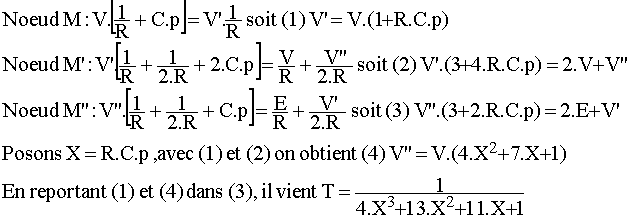
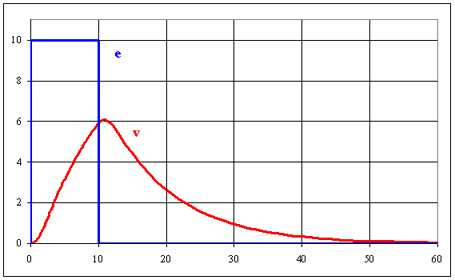
Cherchons la réponse à une impulsion de tension E = 10 V qui dure de t = 0 à T = 10 µs

e(t) = E.[u(t) - u(t-T)] donc E(p) = E/p - E.e^(-p.T)/p et

V(p) = T.E(p) = E.[1-e^(-p.T)]/p.(4.X³+13.X²+11.X+1)

Cherchons les racines de 4.X³+13.X²+11.X+1 = 0

L'utilisation d'une calculatrice donne trois racines réelles : X1 = -1,797 , X2 = -1,350 et X3 = -0,103

4.X³+13.X²+11.X+1 = 4.(X - X1). (X - X2). (X - X3) =4.(R.C)³.(p - a1). (p - a2). (p - a3) avec

a1 =X1/R.C = -1,797.10⁶ , a2 = -1,350.10⁶ et a3 = -0,103..10⁶

On a donc V(p) = [1-e^(-p.T)].[A/p + B/(p - a1) + C/(p - a2) + D/ (p - a3)]

A = p.V(p) en p = 0 soit A = 10 , B = (p - a1).V(p) en p = a1 soit B = -1,83

C = (p - a2).V(p) en p = a2 soit C = 3,32 et D = (p - a3).V(p) en p = a1 soit D = -11,49

Nous en déduisons

v(t) = u(t).[A + B.e^(-a1.t) + C.e^(-a2.t)+D.e^(-a3.t)] - u(t-T).[A + B.e^[-a1(t-T)] + C.e^[-a2(t-T)]+D.e^[-a3(t-T)]]

Nous en déduisons les graphes des grandeurs :