Ce chapitre n'a pas de prétentions mathématiques ; il utilise
les notions
théoriques nécessaires pour utiliser la transformation de
Laplace en électricité
A) Définition
Soit une fonction f(t) définie pour t > 0 et p un nombre
complexe, la transformée de Laplace de f(t) est
la fonction 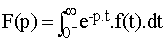
On notera aussi F(p) = L [f(t)]
Cette transformation n'existe pas pour toute fonction car il
faut que l'intégrale converge.
On peut dire qu'il faut que f(t) soit intégrable et qu'elle
n'augmente pas "plus vite" qu'une exponentielle
lorsque t tend vers l'infini.
Remarque 1 : la variable de Laplace p est aussi
notée s
Remarque 2 : l'origine de l'intégrale est prise
à t = 0- pour prendre en compte des fonctions discontinues en t
= 0.
B) Transformées des
fonctions usuelles
Le tableau ci-dessous donne les transformées des fonctions
usuelles :
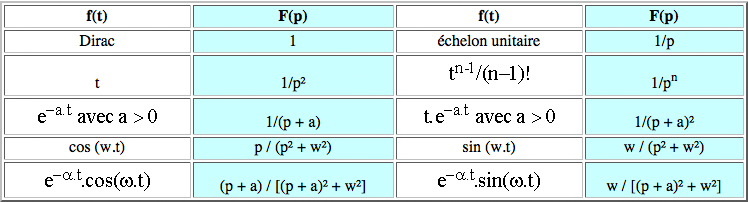
Soit une impulsion de durée T et d'amplitude 1/T donc de surface
unitaire, l'impulsion de Dirac
est la fonction obtenue en faisant tendre T vers 0
Un échelon unitaire est la fonction u(t) qui vaut 0 pour t <
0 et 1our t > 0
C) Propriétés
Linéarité
Soit f(t) et g(t) deux fonctions définies pour t > 0 et deux
constantes K et K', on a :
L [K.f(t) + K'.g(t)] = K. L [f(t)] + K'. L [g(t)]
Théorème du Retard
Soit la fonction f(t).u(t) avec u(t) = 1 pour t > 0 , la
fonction f(t-to).u(t-to) reproduit la fonction f(t) avec un retard
to.
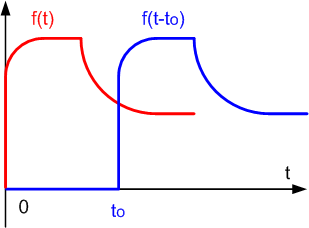
On a :
L [f(t-to).u(t-to)] = e(-to.p).L [f(t).u(t)]
Exemple 1: échelon retardé
Soit un échelon f(t) = E.u(t); on a L [f(t)] = E/p . Si nous
retardons l'échelon de to, il vient :
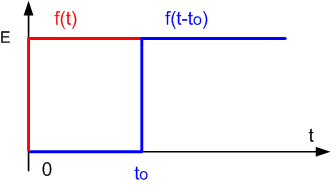
L [f(t-to)] = E.e(-to.p)/p
Exemple 2 : impulsion
Soit l'impulsion représentée ci-dessous :
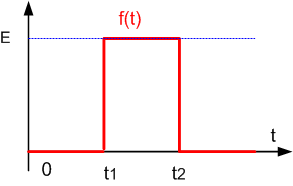
On peut écrire f(t) = E.u(t-t1) - E.u(t-t2) ; en utilisant la
linéarité et le théorème du retard, il vient :
L [f(t)] = E.[ e(-t1.p)/p -
e(-t2.p)/p]
Valeurs finales et initiales
On a : 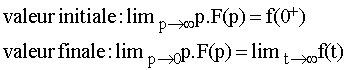
Théorème de la dérivée
Soit f '(t) la dérivée par rapport au temps de la fonction f(t).
On a :
L [f '(t) ] = p. L [f(t)] - f(0- )
Cette formule s'étend aux dérivées successives :
L [f "(t) ] = p². L [f(t)] - p.f(0- ) - f
'(0- )
Si la fonction est nulle pour t < 0, on retrouve un résultat
semblable à celui obtenu par la méthode complexe
en régime sinusoïdal : la transformée de la dérivée se déduit de
celle de la fonction en la multipliant par p.
Théorème de l'intégrale
Soit g(t) la primitive de la fonction f(t) ; on a f(t) = dg/dt
donc L [f(t)] = p.L [g(t)] -g(0- ) ou :
L [g(t) ] = L [f(t)]/p - g(0- )/p

