Lorsque le réseau n'est pas au repos à l'instant t = 0, la dérivation ne se réduit plus à la multiplication par

p et on ne peut plus parler d'impédance opérationnelle.

Il faut alors écrire les équations différentielles puis leur appliquer la transformation de Laplace en tenant

compte des valeurs initiales.

Exemple 5

Soit le réseau ci-dessous, soumis à un échelon de tension e (t) = 10.u (t) avec v (0^- ) = 5 V.

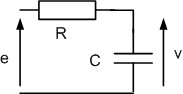
On donne R = 10 kW et C = 100 nF .

e = R.i + v avec i = C.dv/dt ; en appliquant la transformation de Laplace, il vient :

E (p) = 10/p = R.I (p)+.V (p) avec I (p) = C.[p.V (p) -v (0)] soit 10/p = (1+R.C.p).V (p)-5.R.C

V (p) = 10/p. (1+R.C.p)+ 5.R.C/(1+R.C.p) = A/p + (B+5.R.C) /(1+R.C.p)

A = p.V (p) en p = 0 soit A = 10 ; B+5.R.C = (1+R.C.p).V (p) en p = -1/R.C soit B+5.R.C = -5.R.C

Il vient V (p) = 10/p - 5/(p+1/R.C) d'où v (t) = 10 - 5. e^(-t/RC).