On se limite au cas où la fonction F(p) est le quotient de deux polynômes à coefficients réels :

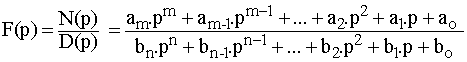avec m < n

La méthode de recherche de la fonction f(t) consiste à décomposer la fonction F(p) en éléments simples à partir de l'analyse des pôles de la fonction, c'est à dire des racines du dénominateur D(p).

Les coefficients des polynômes étant des nombres réels, le dénominateur de degré n à n racines réelles ou complexes; dans ce cas si z = a + j.b est racine, son conjugué z* = a - j.b est aussi racine.

A) Cas d'une racine réelle simple

Supposons que a, nombre réel, soit une racine simple de D(p); cela veut dire que D(p) = (p-a).D'(p) avec D'(a)≠0.

Dans ce cas, on peut écrire F(p) = A/(p-a) + N'(p)/D'p)

La transformée inverse de A/(p-a) donnera le terme E^(a.t) dans f(t).

B) Cas d'une racine réelle multiple

Supposons que a, nombre réel, soit une racine de D(p) d'ordre k : cela veut dire que D(p) est divisible par 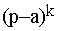: D(p) = 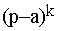.D'(p) avec D'(a)≠0

On peut alors écrire :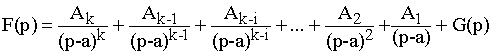

La transformée inverse de 1/(p-a)ⁱ est t^(i-1).e^(a.t)/(i-1)! avec (i-1)! = (i-1)*(i-2)*.(i-3)*...*3*2*1.

Dans la fonction f(t) on aura donc la suite de termes :

C) Cas d'une racine complexe simple

Le nombre complexe -a + j.w est racine de D(p); le nombre conjugué -a - j.w est aussi racine.

La décomposition en éléments simples de F(p) comportera les termes :

D) Calcul de la transformée inverse

Ayant obtenu toutes les racines de D(p) et ayant écrit les fractions correspondantes, il reste à calculer les coefficients Ai apparaissant au numérateur de ces fractions.

Plusieurs méthodes sont possibles :

Réduire les fractions élémentaires au même dénominateur et identifier le numérateur obtenu à celui de la fonction F(p), c'est à dire égaler les coefficients des termes de même degré ; on obtient ainsi 7 équations avec les inconnues A", A', ... ; la résolution de ce système donne la valeur des constantes.

Cette méthode est surtout utilisée lorsque le nombre de termes est faible.

Exemple 1

On peut calculer directement certains coefficients :

Si a est une racine réelle d'ordre k : (p-a)^k.F(p) = N(p)/D'(p) ; en multipliant les éléments simples par (p-a)^k, toutes les fractions ont au numérateur une puissance supérieure ou égale à 1 de (p-a) sauf le terme Ak.(p-a)^k/(p-a)^k = Ak . On en déduit que Ak = N(a)/D'(a);

On peut essayer des "valeurs commodes" de p qui ne sont pas des pôles de D(p).

Par exemple, dans le cas d'un racine complexe -a + j.w, en faisant p = -a , on fait disparaître le coefficient A de l'équation

Exemple 2