Il est assez facile de comprendre qu'une boucle peut osciller puisque le système « se mord la queue ! ».
Supposons que la consigne reste constante et faisons l'hypothèse que la boucle engendre une sinuso´de (superposée à une constante). Nous allons comprendre que cette hypothèse peut se vérifier.
Une sinuso´de apparaissant en Vs se retrouve instantanément en e mais avec un déphasage de - 180° (signe moins du comparateur). Il suffit que, pour la pulsation de cette sinuso´de, l'ensemble correcteur-ampli-processus-capteur introduise à son tour un déphasage de - 180° pour qu'il y ait continuité
Remarque: Ceci ne peut être obtenu que si le processus est au moins d'ordre 3 (ou d'ordre inférieur avec un retard pur).
Si pour cette pulsation le gain de l'ensemble est égal à 1 la sinuso´de est auto-entretenue.
Si ce gain est inférieur à 1 la sinuso´de subit une décroissance exponentielle de son amplitude: dans ce cas la boucle est stable.
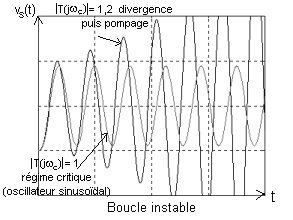
Si ce gain est supérieur à 1 la sinuso´de augmente en amplitude de façon exponentielle: dans ce cas la boucle est instable.
En pratique l'amplitude de l'oscillation ne peut pas augmenter indéfiniment car les saturations de l'amplificateur seront rapidement atteintes et la limiteront. Une oscillation d'amplitude constante mais non sinuso´dale sera alors observée: cette oscillation s'appelle pompage.
Ainsi la pulsation critique wc de l'oscillation sinuso´dale que la boucle peut créer est telle que T(jwc) = -1 (argument de -180° et module de 1).
La pulsation critique wc est donc définie par l'équation ^T(jwc) = -180°.
Rappel : dans ce cours le symbole ^ correspond à l'argument du nombre complexe.
Quatre cas sont possibles:
. Si šT(jwc)š > 1 : la boucle est instable, elle engendre une oscillation d'amplitude divergente jusqu'au pompage limité en amplitude par les saturations de l'amplificateur.
. Si šT(jwc)š = 1 : la boucle engendre une oscillation sinuso´dale. Mais il s'agit d'un régime critique: en pratique ce gain ne peut pas être rigoureusement égal à 1.
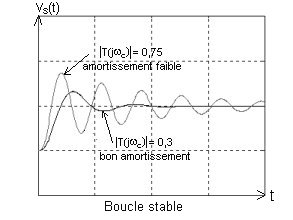
. Si šT(jwc)š < 1 mais proche de 1 (par exemple 0,75): la boucle est stable mais mal amortie (l'amplitude des oscillations diminue peu à chaque pseudo-période).
. Si šT(jwc)š < 1 nettement plus petit que 1 (par exemple 0,3) : la boucle est stable et bien amortie (en une pseudo-période on retrouve pratiquement un régime permanent constant).
Seulement dans ce dernier cas on peut considérer que le système bouclé est un asservissement.
 |  |
La valeur critique du nombre complexe T(jw) est donc -1.
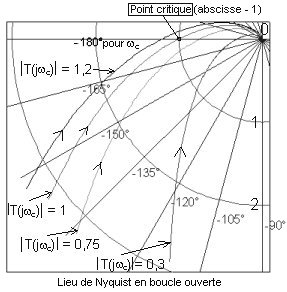
On peut faire une étude graphique de la stabilité de la boucle en représentant le nombre complexe T(jw) (Nyquist ou Black) et en positionnant cette valeur -1 qui sera le point critique. Dans Bode le point critique devient deux axes critiques (-180° et 0 dB).
Ci-dessous sont représentés les 4 cas ci-dessus décrits pour les 3 types de représentation d'un nombre complexe (Nyquist, Black et Bode).
6.2.1 Examinons tout d'abord le lieu de Nyquist de T(jw).
Nous avons représenté le lieu de Nyquist en boucle ouverte pour 4 réglages de gain. Il faut corréler ces quatre lieux avec les quatre comportements en boucle fermée représentés à la page précédente.
La pulsation critique correspond à un argument de - 180°.
Si pour cette pulsation le module est égal à 1 (le lieu de Nyquist passe par le point critique) on est au régime critique: la boucle engendre une oscillation sinuso´dale de pulsation wc.
Si pour la pulsation critique le module est supérieur à 1 la boucle est instable: elle engendre une oscillation d'amplitude divergente jusqu'au pompage.
Si pour la pulsation critique le module est inférieur à 1 la boucle est stable.
Critère du revers: Soit un « micro-observateur » se déplaçant sur le lieu de Nyquist de T(jw) dans le sens croissant des pulsations (sens de la flèche). S'il voit le point critique sur sa droite alors la boucle est instable. S'il voit le point critique sur sa gauche, la boucle est stable.
Dans ce deuxième cas, l'amortissement de la boucle est lié à la distance entre le « micro-observateur » et le point critique: plus cette distance est grande meilleur est l'amortissement de la boucle.
Nous étudierons cette notion de distance entre le lieu de Nyquist et le point critique dans le paragraphe suivant.
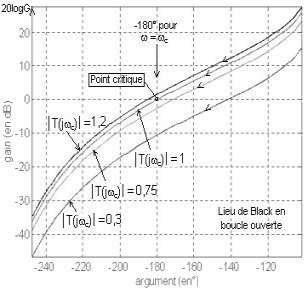
6.2.2 Examinons maintenant le lieu de Black de T(jw).
Cette fois le point critique se trouve à l'intersection des axes -180° et 0 dB.
Nous avons représenté le lieu de Black en boucle ouverte pour les 4 réglages de gain.
Si pour la pulsation critique 20logG vaut 0 dB (le lieu de Black passe par le point critique) la boucle est « juste » instable.
Si pour la pulsation critique 20logG est positif (le lieu passe au dessus du point critique) la boucle est instable.
Si pour la pulsation critique 20logG est négatif (le lieu passe en dessous du point critique) la boucle est stable.
Plus le lieu de Black en boucle ouverte passe bas en dessous du point critique meilleur est l'amortissement en boucle fermée.
Critère du revers: Ici le «: micro-observateur » se déplaçant sur le lieu de Black (dans le sens croissant des pulsations) doit voir le point critique sur sa droite pour que la boucle soit stable.
| 
|
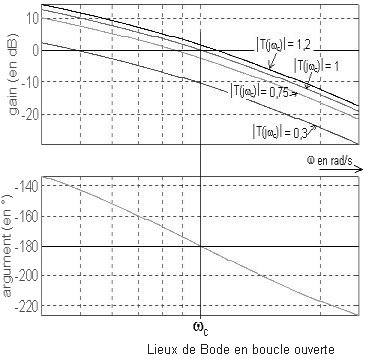
6.2.3 Examinons enfin les lieux de Bode de T(jw).
La courbe de phase est indépendante du réglage de gain puisqu'on le règle par une action proportionnelle K du correcteur (K est un nombre réel, son argument est toujours nul). Par contre la courbe de gain subit une translation (vers le haut si on augmente K). Ainsi, pour un réglage critique tel que 20logšT(jwc)š = 0 dB, la courbe de gain passe par 0 dB pour la pulsation critique, la boucle est "juste" instable.
Si pour la pulsation critique 20logG est positif (la courbe de gain est au dessus de l'axe 0 dB) la boucle est instable.
Si pour la pulsation critique 20logG est négatif (la courbe de gain est en dessous de l'axe 0 dB) la boucle est stable.
Plus, pour la pulsation critique wc, la courbe de gain en boucle ouverte passe bas en dessous de l'axe 0 dB meilleur est l'amortissement en boucle fermée.
|  |
6.2.4 Etude algébrique de la stabilité de la boucle.
La fonction de transfert T(p) en boucle ouverte est imposée. La question posée est : la boucle est-elle stable ?
Il faut tout d'abord remplacer p par jw pour exprimer la transmittance harmonique T(jw) en boucle ouverte et bien sûr exprimer le module šT(jw)š et l'argument ^T(jw) de ce nombre complexe.
Puis il faut résoudre l'équation ^T(jw) = -180°. La solution est unique: c'est la pulsation critique wc.
Enfin il faut remplacer w par wc dans l'expression du module pour obtenir la valeur numérique de šT(jwc)š.
Si šT(jwc)š > 1 : la boucle est instable.
Si šT(jwc)š < 1 : la boucle est stable. Si de plus šT(jwc)š est petit par rapport à 1 (exemple: 0,25), la boucle est bien amortie.
6.2.5 Calcul du réglage critique Kc de l'action proportionnelle K du correcteur.
Cette fois le nombre complexe T(jw) est proportionnel à K (gain réel).
Comme ci-dessus il faut résoudre l'équation ^T(jw) = -180° (l'argument est indépendant de K). La solution est unique: c'est la pulsation critique wc.
Puis on remplace w par wc dans l'expression du module (ce module est proportionnel à K).
Il suffit d'imposer šT(jwc)š = 1 pour en déduire la valeur critique Kc.
Pour ce réglage la boucle est juste instable, elle engendre une oscillation sinuso´dale de pulsation wc.
Pour un réglage K > Kc la boucle est instable: pompage.
Pour K < Kc la boucle est stable.

