A partir de la théorie de Huyghens Fresnel, on va arriver à des simplifications selon Fraunhoffer.
Tout d'abord, on va distinguer 2 cas de diffractions :
- A distance finie ou diffraction de Fresnel (interférence localisée),
- A l'infini ou diffraction de Fraunhoffer (interférence non localisée).
Dans le reste de l'étude, nous nous placerons à l'infini par l'intermédiaire de ce schéma :
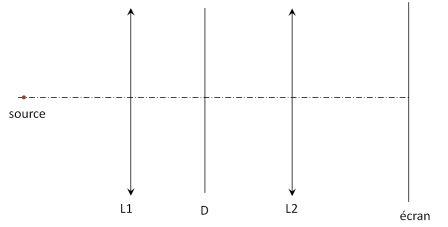
La source est placée dans le plan focal objet de la lentille 1 (création d'un faisceau parallèle);
L'écran sera placé dans le plan focale image de la lentille 2 (visualisation à l'inifini).
Commençons par une ouverture rectangulaire :
On va considérer que l'on place un diaphragme D de largeur a et de longueur b (a<<b) entre une source et un écran de visualisation. La fente aura la forme suivante :
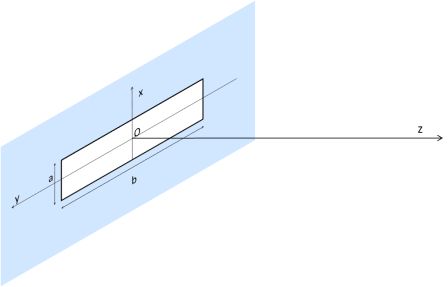
Le phénomène de diffraction n'interviendra que par le coté le plus fin. On se placera donc uniquement dans le plan Oxz, comme dans le schéma simplifié ci-dessous :
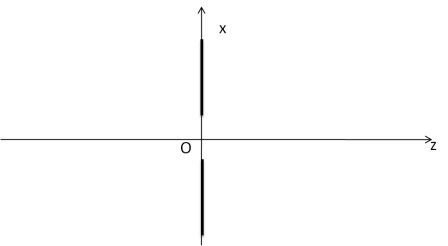
On va découper la fente en mini-fentes de largeur dx (principe de Huyghens Fresnel); alors entre 2 mini fentes successives nous avons 2 rayons dont l'un parcours un temps plus long que l'autre (cf : interférences). Nous avons la différence de marche suivante :
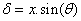avec θ l'angle entre le centre 0 et la position du point M sur l'écran.
En solutionnant l'équation de Huyghens, on trouve que :
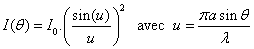
I(θ) étant l'intensité lumineuse suivant l'angle θ.
Cette fonction est représentée ci-dessous :
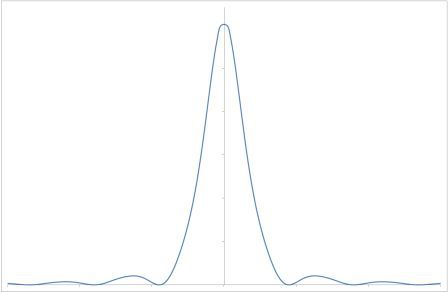
On peut remarquer que :
- la tache centrale est 2 fois plus large que les taches annexes,
- quasiment toute l'intensité lumineuse est concentrée dans la tache centrale.
On peut calculer le diamètre angulaire de la tache centrale et on trouve :
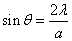
Plus a est petit plus la tache centrale est importante.
Si on fait intervenir la largeur b, on obtient alors pour l'intensité :
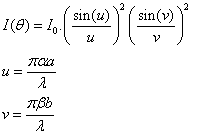
Voyons maintenant pour une ouverture circulaire :
Au vue des symétries du système, il est évident que l'on obtiendra des anneaux et on peut calculer le diamètre angulaire de la tache centrale comme suit :
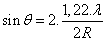
Avec R le rayon du diaphragme.
