Déformées
a) Notions :
Lorsqu'une poutre est soumise à un moment de flexion, elle fléchit. Cette déformée se décompose en une flèche (translation des sections) et une rotation (rotation des sections).
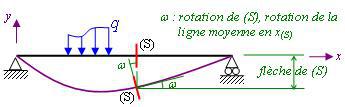
Ces deux paramètres sont intimement liés :
Naturellement, la déformée des structures isostatiques soumises à de la flexion peut se faire par l'intégration suivante :
Il est auparavant nécessaire de déterminer l'équation du moment de flexion (ou les équations du moment de flexion, si la poutre possède plusieurs tronçons).
b) Constantes d'intégration :
En intégrant le moments, des constantes apparaissent. Ces constantes d'intégration se déterminent grâce à des conditions limites (notées CL). En effet, il est possible de connaître la déformée en certains points. Ce sont des valeurs particulières connues de la déformée.
On distingue alors les conditions au niveau des appuis (notées CA), et les conditions de continuité (notées CC).
c) Conditions aux appuis :
Nous connaissons la flèche et parfois la rotation au niveau des appuis. En effet, un appui amène certains blocages :

d) Conditions de continuité :
Les liaisons internes permettent un certain nombre de degrés de liberté. Par conséquent, ils bloquent un certain nombre de mouvements relatifs. On retrouve à peu de choses près le tableau des conditions d'appuis :

A chaque changement de tronçon, on exprime ainsi les relations qui peuvent exister au niveau des déformées du tronçon précédent et du tronçon suivant.
e) Bilan :
Pour les structures isostatiques, on obtient un nombre de conditions limites (CL = CA + CC) identique au nombre de constantes d'intégration.
On peut ainsi résoudre le système et déterminer les équations des rotations et flèches théoriques des structures.
f) Exemple :





