Asymétrie du problème
A priori, la question posée dans la problématique semble symétrique. En effet, si une grandeur
dépend d'une grandeur
selon une relation affine, alors réciproquement
dépend de
selon une relation affine :
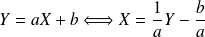pour
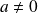
En réalité, la méthode que nous allons développer dans ce cours ne fait pas jouer le même rôle aux grandeurs
et
. Pour comprendre la raison de cette asymétrie, reprenons par exemple le cas des éprouvettes de béton. Expérimentalement, on réalise tout d'abord des éprouvettes ayant une certaine masse volumique
, et on mesure ensuite la valeur de la résistance à la compression
des différentes éprouvettes en les soumettant à un essai destructif. L'objectif de cette expérience est de proposer un modèle permettant de prévoir à l'avance la résistance d'un béton sans avoir à lui faire subir un test destructif. On veut donc connaître
en fonction de
et non pas le contraire.
Définition :
On dit que
est la variable indépendante ou explicative, et que
est la variable dépendante ou à expliquer.
Remarque :
En principe, l'incertitude pesant sur la mesure de
est supposée nulle ou négligeable, tandis que celle sur
est supposée constante (mesures répétées dans les mêmes conditions).
