A) Résistance

Une résistance est une portion de circuit électrique dans laquelle toute l'énergie électrique est transformée en chaleur par effet Joule. Une résistance forme un dipôle électrique c'est à dire une portion de circuit vue entre deux points ou pôles.

Ce dipôle étant étudié avec les conventions d'orientation de la fig.1, nous avons v(t) = R i(t), R étant la résistance du dipôle exprimée en ohm (W).

Cette relation est appelée loi d'Ohm.

D'après les propriétés de la valeur moyenne et de la valeur efficace, nous en déduisons que pour des signaux quelconques, la loi d'Ohm s'applique aux valeurs moyennes V_moy = R.I_moy et efficaces V = R.I.

En régime sinusoïdal, pour i = I.√2.cos (wt), nous avons v = R.I.√2.cos (wt); v et i ont la même phase à l'origine, nous dirons que ces grandeurs sont en phase. Si nous utilisons la représentation de Fresnel, le vecteur 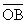associé à v se déduit du vecteur 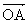associé à i par l'homothétie 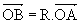. En notation complexe, nous aurons V = R I.

B) Inductance

Une inductance pure est un dipôle dans lequel toute l'énergie électrique est convertie en énergie magnétique.

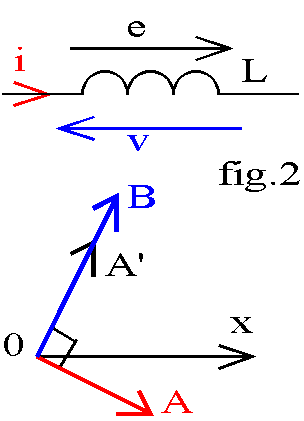
Soit j le flux total à travers le circuit ; nous avons φ = L.i, L étant le coefficient d'inductance propre exprimé en henry (H). Par définition, ce coefficient est toujours positif. Une variation de courant produit une f.é.m induite e = - dj / dt orientée dans le sens de i. Pour un circuit indéformable L est constant donc e = - L.di /dt; si nous comptons la d.d.p en sens inverse de i, il vient v = - e = L.di /dt.

En régime continu, l'intensité i est constante donc la tension v est nulle : une inductance se comporte comme un court-circuit en régime continu.

Si le courant i présentait une discontinuité, la dérivée di /dt tendrait vers l'infini ainsi que la tension; ceci est physiquement impossible : le courant dans une inductance ne peut être discontinu.

En régime périodique, quelle que soit la forme du courant, sa dérivée est de valeur moyenne nulle donc V_moy = 0.

En régime sinusoïdal, associons les vecteurs de Fresnel 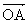à l'intensité i et 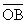à la d.d.p v ; nous savons que le vecteur OA' associé à di/dt se déduit de OA par une rotation de + π/2 et une homothétie de rapport w (fig.2). Nous avons donc OB' = L.OA'. En valeur efficace, nous avons : V = L.w.I; les vecteurs et sont orthogonaux, nous dirons que la tension est en quadrature avant sur le courant ou que le déphasage de la tension sur le courant est

j = (i,v)= (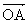,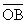)= + π/2.

En notation complexe, nous savons qu'à di / dt est associée la valeur complexe j.w.I ; nous en déduisons la relation V = j.L.w.I. Cette égalité implique l'égalité des modules soit V = L.w.I et l'égalité des arguments soit arg V = arg j.L.w + arg I = π/2 + arg I

C) Condensateur

Un condensateur est un dipôle formé de deux armatures métalliques séparées par un isolant. Si nous créons une charge +q sur une armature en apportant des charges positives ou en enlevant des charges négatives, l'autre armature prend par influence électrostatique la charge opposée -q.

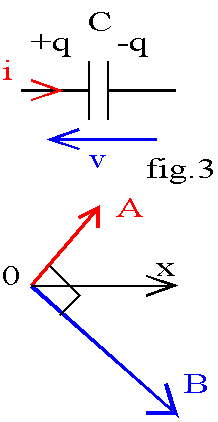
La d.d.p entre les armatures est proportionnelle à la charge électrique : v = θ / C, C étant la capacité du condensateur exprimée en farad (symbole F). L'intensité du courant est lié à la variation de charge :

i = dq / dt soit la relation tension-courant i = C.dv /dt.

En régime continu, la d.d.p est constante donc l'intensité i est nulle : un condensateur se comporte comme un circuit ouvert en régime continu.

Si la tension v présentait une discontinuité, la dérivée dv / dt tendrait vers l'infini ainsi que l'intensité; ceci est physiquement impossible, donc la tension aux bornes d'un condensateur ne peut être discontinue.

En régime périodique, quelle que soit la forme de la tension, sa dérivée est de valeur moyenne nulle donc I_moy = 0.

En régime sinusoïdal, associons les vecteurs de Fresnel 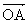à l'intensité i et 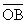à la d.d.p v ; nous savons que le vecteur 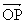associé à la primitive de i se déduit de 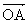par une rotation de -π/2 et une homothétie de rapport 1/w (fig.3). Nous avons donc OB = OP/C. En valeur efficace, nous avons V = I /C.w; les vecteurs 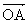et 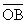sont orthogonaux, nous dirons que la tension est en quadrature arrière sur le courant ou que le déphasage de la tension sur le courant est j = (i,v) = (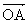,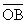)= - π/2.

En notation complexe, nous savons qu'à dv/dt est associée la valeur complexe j.w.V ; nous

en déduisons la relation I = j.C.w.V ou V = I / j.C.w. Cette égalité implique l'égalité des modules soit

V = I / C.w et l'égalité des arguments soit arg V = arg I - arg j.C.w = arg I - π/2.