Un élément piézo-électrique peut être décomposé en une somme d'éléments infinitésimaux ponctuels. (Fig. VII.4)

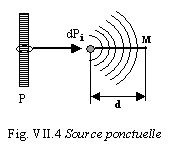
Si la source ponctuelle émet un signal :

v_i(t)   = A.cos(w.t) avec w = 2pF

Le signal reçu au point M est déphasé:

v_iM(t) = A_M.cos(wt + j_i) avec j _i = 2p.d _i /l

L'énergie acoustique résultante au point M est la somme calculée par intégrale

des différentes contributions de  toutes les sources ponctuelles.

 

Lorsque M est situé loin et sur l'axe de propagation, le déphasage j _i varie peu.

Les contributions des différentes sources ponctuelles

arrivent quasiment en même temps au point M. (Fig. VII.5)

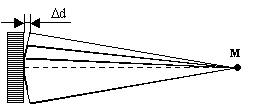
Fig. VII.5 Contributions en un point de l'axe de propagation

 

 

La situation est différente lorsque M s'écarte de l'axe OX (Fig. VII.6)

 

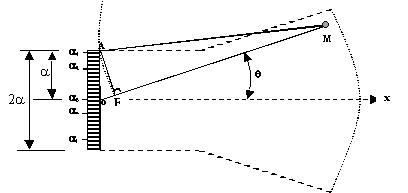
Fig. VII.6 Contributions en un point écarté de l'axe de propagation

 

 

Le point M est écarté de l'axe de propagation OX d'un angle q.

Considérons les éléments infinitésimaux a₁ et a₃ écartés de la distance a

 

la différence OM – AM = OB =a.sin q

 

Si OB = n.l/2  avec n = 1,3,5…

les ondes issues des sources ponctuelles a₁ et a₃ 

arriveront en M en opposition de phase.

Il en sera de même pour a₂ et a₄  et tous les éléments a_i écartés de a

Ce qui se traduit globalement par une énergie nulle en M

 

OB = a.sin q₁ = l /2

pour n = 1

sin q₁ = l / 2a 

Ce phénomène d'annulation se produit pour plusieurs valeurs de n.