La réponse indicielle d'un asservissement bien amorti est caractérisée par son temps de montée tm et par un faible dépassement (par exemple 15%).	La réponse harmonique d'un asservissement bien amorti est caractérisée par sa bande passante à - 6 dB (w-6) et par une faible résonance (par exemple 1,4 dB).

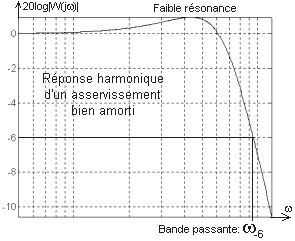La vélocité de l'asservissement pourra être chiffrée soit par la valeur de son temps de montée, soit par la valeur de sa bande passante, sachant que le produit t_m.w_-6 est constant : si on double la bande passante, le temps de montée est divisé par 2.

Les réponses ci-dessus sont comparables à celles d'un système du second ordre bien amorti (par exemple z = 0,5). Pour un système du second ordre on a :  t_m.w_-6 = p.3^1/2 @ 5,44 .
Nous admettrons que pour un asservissement quelconque nous aurons sensiblement le même résultat.
Expérimentalement il est facile de mesurer le temps de montée; c'est plus délicat de mesurer la bande passante (surtout si elle est très faible comme dans le cas d'un asservissement de température).
Par la théorie c'est le contraire: il est très difficile de calculer le temps de montée, alors qu'il est facile de calculer la bande passante.
Nous nous servirons par conséquent de la relation empirique  t_m.w_-6 @ 5,44  pour chiffrer la donnée manquante.

Mais nous avons dit au début du chapitre 6 que nous allons étudier l'ensemble des qualités d'un asservissement en utilisant uniquement l'expression de sa fonction de transfert T(p) en boucle ouverte.
Nous allons comparer ci-dessous la courbe de gain de T(jw) en boucle ouverte et celle de W(jw) en boucle fermée.

Au paragraphe 6.1 nous avons vu :
 T(p) = n(p) / d(p)   et   W(p) = n(p) / [n(p) + d(p)]  donc:
 T(jw) = n(jw) / d(jw)   et   W(jw) = n(jw) / [n(jw) + d(jw)]
 Bien sûr le degré de n(p) est inférieur au degré de d(p) : tous les asservissements sont des filtres passe-bas.
 Donc plus la pulsation w augmente, plus n(jw) devient petit par rapport à d(jw),  d'où:  Pour w grand   W(jw) --> T(jw)
 Ainsi pour w grand par rapport à la bande passante les deux courbes de gain (en boucle ouverte et en boucle fermée) se rejoignent (ainsi que les courbes de phase évidemment).
 Inversement pour w petit, le gain en boucle ouverte est très grand (notamment s'il y a un intégrateur), et de ce fait le gain en boucle fermée est égal à 1 [cette fois c'est d(jw) qui est négligeable par rapport à n(jw)].

Au passage à - 6 dB les deux courbes ne sont pas encore confondues, mais on peut estimer que pour un bon amortissement de la boucle il y a toujours environ un rapport 1,25 entre les deux pulsations w_-6BO et w_-6 (cette dernière pulsation correspondant à la bande passante de l'asservissement).

Le passage des courbes de gain à - 6 dB correspond à un module égal à 0,5  [20log0,5 = -6].
L'étude théorique de la vélocité d'un asservissement consiste donc à résoudre l'équation:
 çT(jw)ç = 0,5 .   La solution de cette équation est  w_-6BO.
 On en déduit la bande passante de l'asservissement :  w_-6 @ 1,25.w_-6BO  ainsi que son temps de montée  t_m @ 5,44 / w_-6 .
De plus, si l'asservissement est bien amorti, la réponse indicielle, (voir la réponse au début du paragraphe), sera pratiquement en régime permanent au bout de 2,5 pseudo-périodes :  t_R = 2,5t_m.
 Remarque: Cette méthode ne permet pas de calculer précisément le temps de montée de l'asservissement puisqu'on fait deux approximations empiriques: d'abord le coefficient 1,25 puis le coefficient 5,44.  Aussi il faut arrondir les résultats obtenus.