Schéma de boucle :
Régulateur de type
série :

Relation au niveau argument du
transfert de boucle ouverte à la pulsation

:
Relation en module pour la pulsation

afin d’avoir une marge de gain de

:
- Bilan 1 : Régulateur P
soit
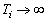 et
et 
Système à résoudre

soit 2 équations et 2 inconnues

- Bilan 2 : Régulateur PI soit

Système à résoudre

soit
2 équations et 3 inconnues

Système à résoudre

soit
2 équations et 4 inconnues

Régulateur P :
Pour résoudre l’équation transcendante en argument, nous pouvons faire
l’hypothèse à vérifier en application que la pulsation

est
« grande » ce qui entraîne un déphasage de la partie 1
er
ordre du modèle de Broïda voisin de

.

et

Régulateur PI :
Pour résoudre « facilement » les équations, nous pouvons faire une
hypothèse de compensation zéro-pôle en introduisant l’équation supplémentaire

Régulateur PID :
Pour résoudre le système, nous devons introduire 2 équations supplémentaires,
nous conservons la compensation zéro-pôle (

) et
nous utilisons l’action dérivée pour avoir un apport de phase de


Ces considérations terminent le
cours AU3, les résultats étant donnés sous forme de fonctions de transfert notamment
au niveau des correcteurs et régulateurs sont relatifs au domaine analogique.
Ils vont être étendus à une structure numérique dans le module complémentaire
AS21.

