L'hypothèse alternative :

H1 est alors une partie seulement du contraire de H0 (un côté seulement).

Cette hypothèse alternative consiste alors à dire que p et f sont trop éloignées (le contexte laissant supposer qu' à priori p sera supérieur à f ou bien f supérieur à p) l'une de l'autre pour que cette différence soit due au hasard (on dit aussi due aux fluctuations d'échantillonnage).

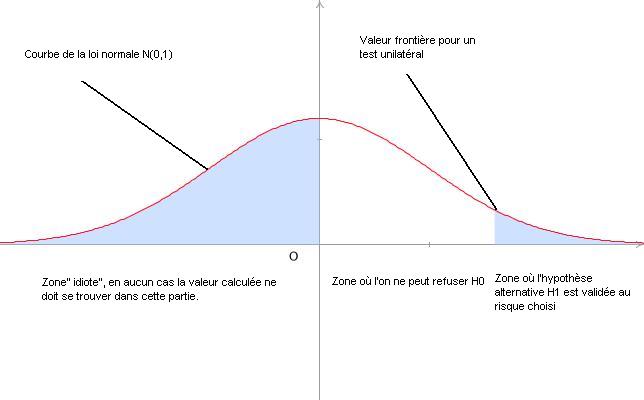
Nous supposons maintenant que le côté à tester est celui où le contexte laisse supposer qu'à priori, f est plus grande que p.

L'autre côté sera appelé la "zone idiote", zone où il sera donc (en raison du contexte) impossible de se trouver à priori.

On lit alors dans la table de la loi normale réduite le nombre 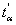tel que :

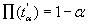
En savoir plus

Par exemple, si le risque est de 5 %, on trouvera 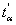=1,65.

On peut alors conclure :

• Si t est dans l'intervalle ]0 ; 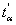[, alors on ne peut refuser H0 (il y a conformité).
• Si t n'est pas dans l'intervalle ]0 ; 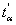[ tout en étant positif, alors, on refuse H0 au risque 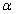(il n'y a pas conformité).

Il est exclus à priori que t soit négatif (à gauche de 0).