A ) Puissance active

Soit un dipôle alimenté sous la tension v(t) = V.√2.sin(w.t) et introduisant un déphasage (j,v) = j . L'intensité est j (t) = J√2.sin (w.t-j) et la puissance instantanée p (t) = v (t).j (t) = 2.V.J.sin (w.t).sin (w.t-j).

En utilisant la formule trigonométrique 2.sin (p).sin (θ) = cos (p - θ) -cos (p + θ), il vient :

p (t) = V.J.cos (j) - V.J.cos (2.w.t-j), somme d'un terme constant et d'un terme sinusoïdal de fréquence 2.f, appelé puissance fluctuante. La puissance active est la moyenne sur une période de cette puissance instantanée. La puissance fluctuante étant alternative, sa valeur moyenne est nulle d'où P = V.J.cos (j).

B) Facteur de puissance

F_p = P / S = cos (j) . Il ne dépend que du déphasage introduit par le dipôle.

La connaissance du facteur de puissance ne suffit pas à déterminer le déphasage car cos (j) = cos (-j); on ajoutera à la valeur du facteur de puissance la mention AR si j > 0 (dans ce cas l'intensité est en retard sur la tension) et AV si j < 0 (dans ce cas l'intensité est en avance sur la tension).

C) Puissance réactive

Dans le cas du régime sinusoïdal, on associe à la puissance active P, la puissance réactive θ = V.J.sin (j)

Cette puissance ne peut être transformée en énergie utilisable, elle est dit fictive et ne sert que dans les calculs. Pour la distinguer des puissances active et apparente, on l'exprime en vars (symbole VAR).

D) Puissance complexe

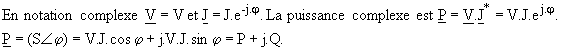
Le calcul en complexe permet donc de calculer simultanément les trois puissances active, réactive et apparente. Les relations entre les formes rectangulaire et polaire donnent :

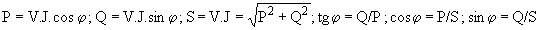
Dans le cas où le dipôle se réduit à une impédance :