Grâce à cet artifice, outre l'avantage d'avoir une représentation du rapport plus dilatée, apparaît celui, énorme, que pour un système électronique donné les quantités G_P, G_v et G_i  sont  égales (exclusivement dans le cas où les résistances d'entrée et de sortie dans lesquelles P_S et P_e sont dissipées sont égales). En effet :

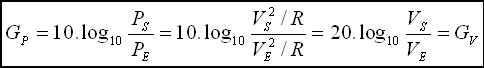(2-3)

On établit la même relation d'égalité entre G_P et G_i et  évidemment entre G_v et G_i. Cette observation est particulièrement intéressante dans le domaine des moyennes et hautes fréquences où l’identité des résistances d'entrée et de sortie des fonctions est en général assurée (notion d'adaptation d'impédance) : un amplificateur, par exemple, aura son gain en puissance et son gain en tension exprimés par la même quantité en décibel. Autrement dit on pourra additionner les coefficients de transmission, exprimés en dB, d'une suite de fonctions et décider seulement à la fin de l'évaluation que l'on désire connaître un rapport de  puissance, de tension, voire de courant. 

            Par contre dès que la notion d'adaptation d'impédance disparaît il vaut mieux utiliser les notions de tension d’entrée et de tension de sortie. C’est ainsi que, dans le domaine des amplificateurs opérationnels, la notion de gain en puissance n'a généralement pas d'intérêt. Dans ce cas en effet l'équivalence G_PdB-G_VdB disparaît complètement vu la différence des résistances d'entrée et de sortie des fonctions.

            Notons pour finir cette introduction que :

-         0dB correspond à une fonction ayant un coefficient de 1 (ce qui est évident si on remarque que le zéro est l'élément neutre de l'addition comme le 1, celui de la multiplication).

 -         les amplifications sont représentées par des nombres positifs. 

-         les affaiblissements sont représentés par des nombres négatifs. 

-         un gain de 10 (coefficient 10) et une atténuation de 10 (coefficient 0,1) sont représentés par deux quantités de signe opposé mais de modules égaux. 

-         à titre anecdotique, le décibel, qui est en principe le dixième du Bel est une référence à part entière puisque selon les cas il est défini par 10 log₁₀ (cas des puissances) ou 20 log₁₀ (cas des tensions et des courants par exemple) pour homogénéiser les valeurs numériques.