On applique maintenant un échelon de vitesse de commande: x=a.t.u(t) donc X=a/p2.
3.4.1 Dérivateur
T(p) = p d'où: Y(p) = p.[a/p2] = a/p donc: y(t) = a.u(t). C'est un échelon d'amplitude a (correspondant à la pente de la rampe de commande).
3.4.2 Intégrateur
T(p) = 1/p d'où: Y(p) = [1/p].[a/p2] = a/p3 donc: y(t) = a.t2/2.u(t).
C'est une parabole (de position), donc un échelon d'accélération de a unités par seconde-carré.
3.4.3 Premier ordre
Pour que la pente de la rampe de sortie ait la même pente que la commande il faut que le gain A en position (statique) du système soit de 1. Pour une valeur quelconque du gain A la réponse est de pente différente que celle de la rampe de commande (si A<1 elle est plus petite, si A>1 elle est plus grande). Donc si A est différent de 1 les fonctions x(t) et y(t) s'éloignent l'une de l'autre. Au contraire si A=1, en régime établi, les deux rampes ont même pente et il apparaît alors une erreur de traînage e1.
T(p) = Y/X = 1/(1+ tp) d'où: Y(p) = [1/(1+ tp)].[a/p2] = a/[p2(1+tp)]
donc: y(t) = a[t - t + t.e-t/t ]u(t) .
En régime établi (au bout de 7t) c'est une rampe retardée d'un temps t par rapport à x(t). |
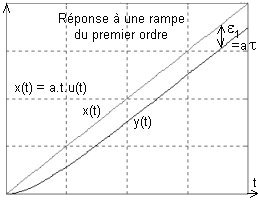 |
Erreur de traînage e1 = lim [x(t) - y(t)]t-->µ = lim [p(X - Y]p-->0 = lim p{a/p2 - a/[p2(1+tp)]}p-->0 = lim [at/(1+tp)]p-->0 = at
L'erreur de traînage est proportionnelle à la constante de temps du système.
Ainsi, si le système du premier ordre est un capteur dont la précision statique est supposée excellente, la mesure d'une grandeur qui varie en forme de rampe peut être erronée si la constante de temps du capteur n'est pas négligeable. Pour une régulation la constante de temps du capteur n'a pas d'importance capitale. Par contre pour un asservissement où la consigne varie en permanence, il faut que la constante de temps du capteur soit négligeable (en pratique 100 fois plus petite que la plus grande constante de temps du processus).
3.4.4 Second ordre
De la même façon que pour le premier ordre, nous allons étudier la réponse du second ordre dont le gain en position (statique) est égal à 1.
T(p) = Y/X = 1/(1+2zp/w0 + p2/w02) d'où
Y(p) = a/[p2(1+2zp/w0 + p2/w02)].
On obtient y(t) = a[t - 2z/w0 + e-t/t.q(t)]u(t)
où q(t) est une fonction sinusoļdale de pulsation wp.
En régime établi (au bout d'un temps 7/zw0) , y(t) est une rampe retardée d'un temps 2z/w0 par rapport à x(t).
Erreur de traînage: bien sûr si l'on dispose de la fonction du temps, pour obtenir sa limite on fait tendre t vers l'infini. Utilisons néanmoins le théorème de la valeur finale pour déterminer cette erreur de traînage: |
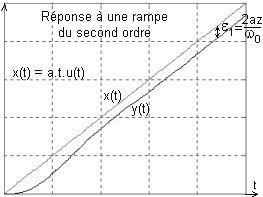 |
e1 = lim [x(t) - y(t)]t-->µ = lim [p(X - Y]p-->0 = lim p{a/p2 - a/[p2(1+2zp/w0 + p2/w02)]}p-->0
= lim [a(2z/w0+p/w02)/(1+2zp/w0 + p2/w02)]p-->0 = 2az/w0.

