Les quartiles partagent l'effectif en quatre parties, chacune d'entre elles représentant le quart de l'effectif total.

Le premier quartile est la valeur notée Q₁ du caractère qui partage l’effectif total en deux groupes, le premier, constitué des valeurs inférieures ou égales à Q₁ ayant un effectif  égal au quart de l’effectif total, le deuxième, constitué des valeurs supérieures  ou égales à Q₁ ayant un effectif  égal aux trois quarts de l’effectif total.

Le troisième quartile est la valeur notée Q₃ du caractère qui partage l’effectif total en deux groupes, le premier, constitué des valeurs inférieures ou égales à Q₃ ayant un effectif  égal aux trois quarts de l’effectif total, le deuxième, constitué des valeurs supérieures  ou égales à Q₁ ayant un effectif  égal au quart de l’effectif total.

Le deuxième quartile est la médiane... 

 

 

Rappelons le tableau donné dans le vocabulaire pour décrire.

 

Salaire	[1,2 ; 1 ,8[	[1,8 ; 2,3[	[2,3 ; 2,7[	[2,7 ; 33[	[3,3 ; 4,1[	[4,1 ; 4,8[
Effectifs	53	43	41	22	16	9
Effectifs cumulés croissants	53	96	137	159	175	184

On commence d’abord par déterminer la classe du premier et du troisième quartile, comme dans le cas discret, en utilisant les effectifs cumulés croissants par exemple.

La classe du premier quartile est [1,2 ; 1,8[, celle du troisième est [2,7 ;3,3 [ .

On doit ensuite réaliser, comme pour la médiane, des interpolations linéaires, de façon à trouver les valeurs des quartiles.

Entrainez vous à tracer la droite d'interpolation comme pour la médiane.

Voici les calculs :

 

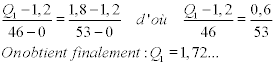
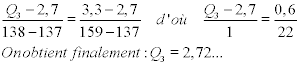
Interprétation :

Un quart des salariés gagne moins de 1,7 K€ brut mensuel ,les trois quarts gagnent plus, donc Q1=1,7K€ (arrondi).

Trois quarts des salariés gagnent moins de 2, 7 K€ brut mensuel ,un quart gagne plus, donc Q3=2, 7 K€ (arrondi).

Remarque :

Le deuxième quartile est égal à la médiane Me