Le cas continu
Définition
C’est la valeur notée Me du caractère qui partage l’effectif total en deux groupes, chacun ayant un effectif égal à la moitié de l’effectif total (à une unité près).
Exemple : le salaire brut mensuel
Rappelons le tableau donné dans le vocabulaire pour décrire.
|
Salaire |
[1,2 ;
1 ,8[ |
[1,8 ; 2,3[ |
[2,3 ; 2,7[ |
[2,7 ; 33[ |
[3,3 ; 4,1[ |
[4,1 ; 4,8[ |
|
Effectifs |
53 |
43 |
41 |
22 |
16 |
9 |
|
Effectifs
cumulés croissants |
53 |
96 |
137 |
159 |
175 |
184 |
On commence d’abord par déterminer la classe médiane, comme dans le cas discret, en utilisant les effectifs cumulés croissants par exemple.
La classe médiane est donc ici [1,8 ; 2,3[.
Quand c’est possible, on détermine ensuite la valeur de la médiane par interpolation linéaire. Pour cela, il faut être sûr que la répartition des individus est régulière à l’intérieur de la classe. Ici, il n'y a aucune raison que ce ne soit pas le cas, alors qu'il est possible que, par effet de seuil, tous les salariés soient au sommet de la tranche (ou classe)...
Il est alors possible d'écrire l'équation du premier degré suivante :
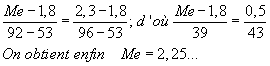
Interprétation :
La moitié des salariés gagne moins de 2,25 K€(on a arrondi...) l'autre moitié, plus !
Remarque
La médiane est un centre du point de vue des effectifs.
La médiane n'est pas sensible à la présence d'une valeur "hors normes" ou extraordinaire.