Variance et écart-type
Définition : Variance
On définit la variance d'une série continue
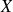comme la variance de la série classée associée :
Remarque :
Comme dans le cas des séries discrètes, la variance d'une série continue est d'autant plus grande que les valeurs de cette série sont très éparpillées autour de la valeur moyenne.
Définition : Écart-type
L'écart-type d'une série continue
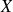est la racine carrée de la variance de cette série, de sorte qu'elle est de même dimension que les valeurs de cette série.
Exemple :
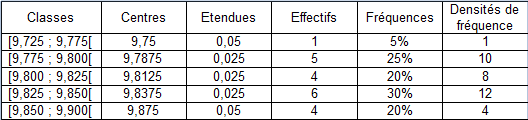
La variance et l'écart-type d'une série continue sont assimilés aux paramètres correspondants de la série classée associée. Dans le cas de la série
et avec la formule de Koenig, on a donc :
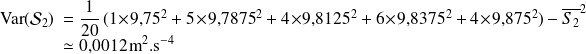
D'où l'écart-type :
Ainsi, les valeurs mesurées pour
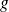étaient, en moyenne, égales à
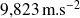avec un écart moyen par rapport à cette moyenne de l'ordre de
.
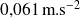