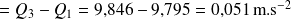Étendue et écart inter-quartiles
Définition : Étendue
L'étendue d'une série statistique peut se définir, toujours à partir de la série classée, de deux façons :
Soit comme la différence entre la limite supérieure
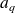de la dernière classe et la limite inférieure
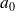de la première classe. C'est la définition que nous utiliserons dans le cadre de ce cours : étendue
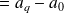.Soit comme la différence entre le centre
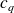de la dernière classe et le centre
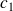de la première classe : étendue
.
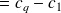Définition : Écart inter-quartile
L'écart inter-quartiles d'une série continue se définit de la même manière que celui d'une série discrète, comme la différence entre le troisième et le premier quartiles.
Exemple :
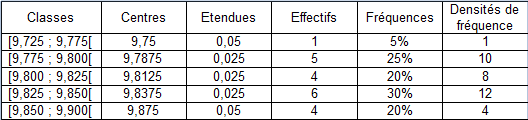
L'étendue de la série statistique correspond, chez les séries discrètes, à la différence entre la plus grande valeur recueillie et la plus petite valeur. Or, dans le cas des séries continues, on passe par l'intermédiaire d'une série classée afin de ne pas avoir à prendre en compte toutes les modalités observées (qui sont en très grand nombre en général). Cependant, pour éviter de sous-estimer la différence entre la plus grande et la plus petite des valeurs recueillies, on n'a pas intérêt à assimiler l'étendue de la série continue à celle de sa série classée (c'est-à-dire à la différence entre le plus grand centre de classe et le plus petit). Au contraire, on préfère souvent surestimer cette différence en l'assimilant à la différence entre la limite supérieure de la dernière classe et la limite inférieure de la plus petite classe.
Dans le cas de la série
, on a donc :
en travaillant avec les limites de classe, étendue
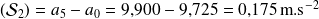
en travaillant avec les centres, étendue
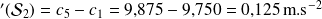
Pour compléter l'information donnée par l'étendue, on peut calculer, comme dans le cas des séries discrètes, l'écart inter-quartiles : écart inter-quartile
