Regroupement en classes
Lorsque le caractère étudié d'une série statistique peut prendre a priori n'importe quelle valeur dans un intervalle
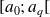, on regroupe ces valeurs suivant des classes
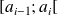choisies en fonction de l'étude menée et auxquelles on ajoute les intervalles
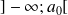et
.
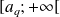On définit pour chaque classe
:
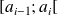les limites
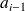et
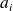de la classe ;le centre
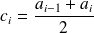de la classe ;l'amplitude
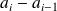;l'effectif
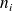et la fréquence
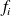de la classe.
On remplace alors l'étude de la série continue initiale par la série discrète constituée des modalités
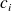affectées des effectifs
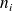. On appelle série classée la série ainsi obtenue.
Exemple :
Au cours d'une séance de TP visant à mesurer expérimentalement la constante d'accélération de la pesanteur
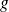, 20 étudiants ont chacun obtenu une mesure. La liste de valeurs ainsi récoltées forme une série statistique continue
. Un regroupement en classes des valeurs de cette série conduit au tableau suivant :
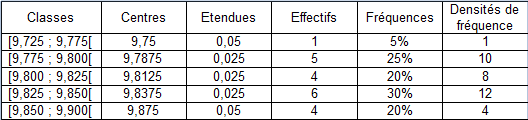
Grâce à ce regroupement, on peut assimiler la série statistique continue
à une série discrète dont les modalités sont les centres des classes auxquels on affecte les effectifs des classes. Cette approximation est pertinente à condition que les centres des classes soient des valeurs représentatives, c'est-à-dire que les valeurs observées dans chaque classe s'y répartissent à peu près uniformément.
