L'abstention comme réponse possible - Partie 8
Attention, votre navigateur ne supporte pas le javascript ou celui-ci a été désactivé. Certaines fonctionnalités dynamiques de ce module sont restreintes.
Un étudiant répond à un QCU (Questionnaire à Choix Unique) de mathématiques sur les probabilités. On s'intéresse au score que peut obtenir cet étudiant en répondant au hasard à un QCU de 10 questions indépendantes. A chaque question correspondent 4 propositions dont une seule est correcte ; trois éventualités se présentent alors :
si l'étudiant coche la bonne réponse, il empoche 2 points
s'il coche une mauvaise réponse parmi les trois, il perd 1 point
s'il s'abstient, le score n'est pas modifié (aucun point n'est gagné ni perdu)
L'étudiant choisit au hasard parmi ces 5 possibilités (abstention ou choix d'une des quatre réponses proposées) pour chaque question.
On note, pour un entier i variant de 1 à 10, Xi la variable aléatoire discrète représentant le nombre de points obtenus par l'étudiant à la question n°i.
On note par ailleurs Z la variable aléatoire représentant la note finale obtenue par cet étudiant.
Quelle est la note finale que l'étudiant peut "espérer" obtenir en ayant répondu au hasard (y compris en s'abstenant) aux 10 questions ? (Penser à faire défiler l'écran vers le bas si la résolution d'écran ou la taille de la fenêtre ne permettent pas l'affichage de toutes les propositions...)
La question posée revient à calculer l'espérance de la variable Z. Or, la note finale étant obtenue en ajoutant les scores obtenus à chacune des questions :
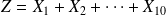
On peut donc s'appuyer sur la propriété de linéarité de l'espérance pour calculer
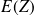 :
: