L'abstention comme réponse possible - Partie 2
Attention, votre navigateur ne supporte pas le javascript ou celui-ci a été désactivé. Certaines fonctionnalités dynamiques de ce module sont restreintes.
Un étudiant répond à un QCU (Questionnaire à Choix Unique) de mathématiques sur les probabilités. On s'intéresse au score que peut obtenir cet étudiant en répondant au hasard à un QCU de 10 questions indépendantes. A chaque question correspondent 4 propositions dont une seule est correcte ; trois éventualités se présentent alors :
si l'étudiant coche la bonne réponse, il empoche 2 points
s'il coche une mauvaise réponse parmi les trois, il perd 1 point
s'il s'abstient, le score n'est pas modifié (aucun point n'est gagné ni perdu)
L'étudiant choisit au hasard parmi ces 5 possibilités (abstention ou choix d'une des quatre réponses proposées) pour chaque question.
On note, pour un entier i variant de 1 à 10, Xi la variable aléatoire discrète représentant le nombre de points obtenus par l'étudiant à la question n°i.
On note par ailleurs Z la variable aléatoire représentant la note finale obtenue par cet étudiant.
Quelle est la loi de probabilité suivie par chaque variable Xi ? (Penser à faire défiler l'écran vers le bas si la résolution d'écran ou la taille de la fenêtre ne permettent pas l'affichage de toutes les propositions...)
L'analyse du support permet d'éliminer les 3 premières propositions :
une variable suivant une loi de Bernoulli a pour support l'ensemble
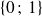
une variable suivant une loi binomiale a pour support un ensemble du type
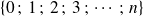où
est un nombre entier strictement positif fixéune variable suivant une loi géométrique a pour support l'ensemble des entiers naturels
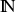
De plus, comme il y a 3 fois plus de chance de choisir une mauvaise réponse que de s'abstenir ou de choisir la bonne réponse, on peut aussi éliminer la loi discrète uniforme.
