Définition :
La fonction 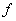 admet un minimum relatif en admet un minimum relatif en 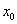 si il existe un intervalle du type si il existe un intervalle du type 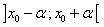 , , 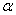 étant strictement positif, tel que étant strictement positif, tel que
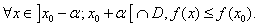
La fonction 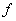 admet un minimum absolu en admet un minimum absolu en 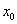 si il existe un intervalle du type si il existe un intervalle du type 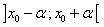 , , 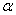 étant strictement positif, tel que étant strictement positif, tel que
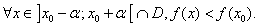
Définition :
La fonction 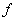 admet un maximum relatif en admet un maximum relatif en 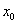 si il existe un intervalle du type si il existe un intervalle du type 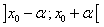 , , 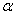 étant strictement positif, tel que étant strictement positif, tel que
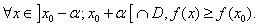
Définition :
La fonction 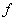 admet un maximum absolu en admet un maximum absolu en 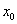 si il existe un intervalle du type si il existe un intervalle du type 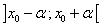 , , 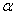 étant strictement positif, tel que étant strictement positif, tel que
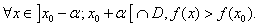
Un extremum est un maximum ou un minimum.
Théorème :
Si la fonction 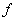 admet un extremum en admet un extremum en 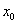 et qu’elle est dérivable en et qu’elle est dérivable en 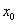 , alors , alors 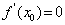
Réciproquement :
Théorème :
Si la fonction 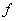 est dérivable sur un intervalle est dérivable sur un intervalle 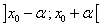 , , 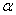 étant strictement positif, et si la fonction étant strictement positif, et si la fonction 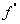 s’annule en s’annule en 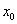 en changeant de signe, alors la fonction en changeant de signe, alors la fonction 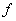 admet un extremum relatif en admet un extremum relatif en 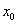 . .
|

