Soit 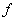 une fonction réelle d’une variable réelle définie au voisinage de une fonction réelle d’une variable réelle définie au voisinage de 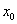 , c'est-à-dire sur un intervalle de la forme , c'est-à-dire sur un intervalle de la forme 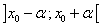 , , 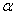 étant strictement positif. étant strictement positif.
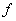 est continue en est continue en 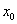 . Soit C la courbe représentative de . Soit C la courbe représentative de 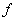 dans le plan P rapporté au repère dans le plan P rapporté au repère 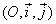 . Soit . Soit 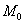 le point de C d’abscisse le point de C d’abscisse 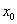 . Soit x un point de . Soit x un point de 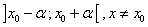 et M le point de C dont l’abscisse est x. et M le point de C dont l’abscisse est x.
On a donc 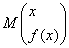 et et 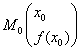 . .
Soit 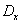 la droite la droite 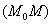 dont le coefficient directeur est dont le coefficient directeur est 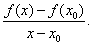
La courbe C admet une tangente en 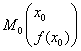 si (et seulement si) la droite si (et seulement si) la droite 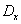 a une position limite D quand a une position limite D quand 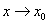 . .
D est la tangente à C en 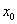 . .
L’équation de la tangente est alors, si la fonction f est dérivable en 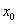 , ,
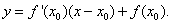
Si 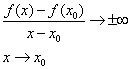 alors la courbe C admet une tangente « verticale » d’équation alors la courbe C admet une tangente « verticale » d’équation 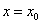
On peut définir une « demi tangente » à droite ou à gauche en utilisant la définition de la demi dérivée à droite ou à gauche en 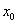 . . |

