A) Méthode générale

La forme générale des équations différentielles linéaires à coefficients constants que l'on doit résoudre en électricité est :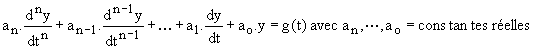

La résolution se fait en cinq étapes :

1) Forme canonique

Les systèmes étudiés, les grandeurs à calculer et les coefficients peuvent prendre des formes diverses suivant le réseau. Pour avoir une résolution type, on définira une mise en forme particulière de l'équation donnant une expression identique dans tous les cas; cette expression sera dite forme canonique de l'équation. Elle ne dépendra que de l'ordre de l'équation.

2) Equation sans second membre

Dans l'équation étudiée, on donnera à g (t) la valeur 0. Puis on devra résoudre l'équation. La forme de la solution y₁ (t) de l'équation sous forme canonique ne dépend également que de l'ordre de l'équation.

L'intégration fera apparaître un nombre n de constantes arbitraires égal à l'ordre de l'équation.

Dans la majorité des systèmes physiques, y₁ (t) ® 0 quand t® ¥ ; la solution y₁ (t) n'intervient donc que durant le régime transitoire.

3) Solution particulière

On doit trouver une fonction y₂ (t) solution de l'équation avec second membre.

Le système étant linéaire, on cherche une solution de même forme que g (t). Cette recherche se fait par identification. On écrit avec des coefficients arbitraires une fonction y₂ de même forme mathématique que g (t), on calcule 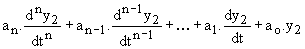et on l'identifie à g (t), c'est à dire que l'on cherche la valeur à donner aux coefficients arbitraires pour que 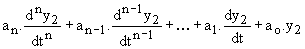= g (t) pour toute valeur de t.

Si g (t) = K = Cste , on cherche y₂ = K' = Cste; toutes les dérivées étant nulles, il vient : K' = K/a_o

Si y (t) est un polynôme de degré n, on cherche un autre polynôme de degré n:

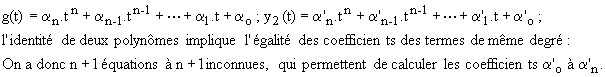
Par exemple si 2.dy/dt + y = 20.t² - 2.t - 20 ; posons y₂ = a.t² + b.t + c, il vient :

2.(2.a.t+b) + a.t² + b.t + c º 20.t² - 2.t - 20 soit a = 20 ; 4.a+b = -2 et 2.b + c = -20 ;

d'où b = -2 - 4.a = -82 ; c = -20 - 2.b = 144.

g (t) est une fonction sinusoïdale de fréquence f, on cherche une fonction sinusoïdale de même fréquence :

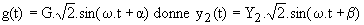
On sait que la méthode complexe permet de résoudre les opérations sur les grandeurs sinusoïdales de même fréquence :

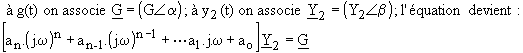
On se limitera à ces types de fonctions qui sont les plus fréquentes en électricité

4) Solution générale

La solution générale de l'équation est y (t) = y₁ (t) + y₂ (t)

5) Constantes d'intégration

Si mathématiquement l'équation a une infinité de solutions différentes en raison de la présence des constantes d'intégration, physiquement le réseau ne peut avoir qu'un état. Les valeurs des constantes d'intégration devront donc être calculées à partir des valeurs initiales des grandeurs du réseau.

B) Equation du premier ordre

La forme générale de l'équation différentielle du premier ordre est : .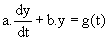

Si b = 0, la résolution se limite à un calcul de primitive : .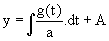

Nous supposerons par la suite a et b non nuls.

1) Forme canonique

la forme canonique est caractérisée par un coefficient 1 pour la fonction; elle s'obtient en divisant par a les deux membres :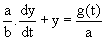

On pose: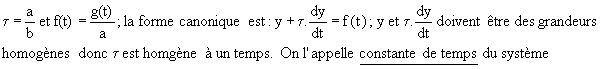

2) Equation sans second membre

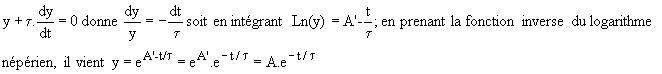
3) Solution particulière

On applique la méthode d'identification :

Si f(t) = K = Cste , on cherche y₂ = K' = Cste; 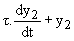=K' identique à K donc la solution particulière est y₂ = K.

Si y (t) est un polynôme de degré n, on cherche un autre polynôme de degré n:

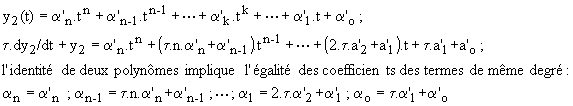
Si f(t) est une fonction sinusoïdale de fréquence f, on cherche une fonction sinusoïdale de même fréquence :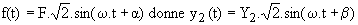

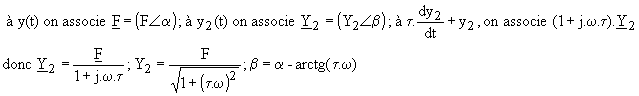
4) Solution générale

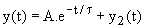
5) Calcul de la constante d'intégration

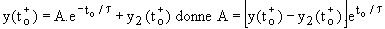
La fonction exponentielle étant continue, il n'est pas nécessaire de distinguer ses valeurs pour .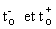

 

Exemple :

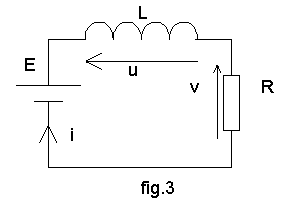
On étudie le réseau ci-dessus : R = 1 kW et L = 1 mH.

Pour t < 0 on a E = -12 V et on a atteint le régime permanent continu. Pour t > 0, on a E = 12 V.

Pour t < 0, en régime continu, l'inductance est un court-circuit donc u = 0 et v = R.i = E soit i (0^- )= -12 mA.

i est variable d'état donc i(0⁺) = i(0^- ) = -12 mA. Nous en déduisons v(0⁺) = R. i(0⁺) = -12 V et u(0⁺) = E - v = 24 V.

Pour t > 0, les équations du réseau sont : E = u + v ; v = R.i et u = L.di/dt ; nous en déduisons

L.di/dt + R.i = E, équation différentielle d'ordre 1. En divisant par R, nous obtenons la forme canonique i + t.di /dt = E/R avec t = L/R = 1 µs.

Le second membre étant constant, la solution est de la forme : .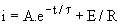

La valeur initiale étant i(0) = -12 mA, il vient : A = [i (0) - E/R].e⁰ = -24 mA.

Nous en déduisons .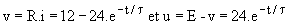

Le régime permanent sera atteint lorsque les grandeurs seront continues donc théoriquement pour t® ¥ ; en pratique pour t = 5.t, exp(^-5) = 6,7/1000 << 1 ; on pourra considérer que le régime permanent est quasi atteint à cette date.

C) Equation du second ordre

La forme générale de l'équation différentielle du second ordre est :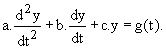

On supposera que tous les coefficients sont différents de 0 et positifs.

1) Forme canonique

la forme canonique est caractérisée par un coefficient 1 pour la dérivée seconde.

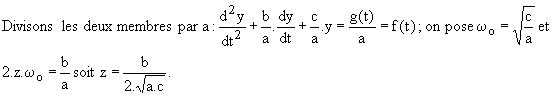
La forme canonique est donc : 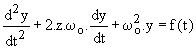; w_o est la pulsation propre et z est le coefficient d'amortissement.

2) Equation sans second membre

On doit d'abord rechercher les racines de l'équation caractéristique : .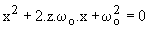

Le déterminant réduit de l'équations est 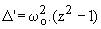. On aura donc 3 cas :

Premier cas : z > 1 ; l'équation caractéristique a alors deux racines réelles négatives:

.

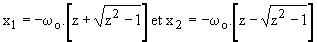La solution générale est de la forme :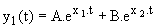

Deuxième cas : z = 1 ; l'équation caractéristique a alors une racine double -w_o. Dans ce cas la solution générale est :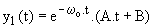

Troisième cas : z < 1 ; l'équation caractéristique a deux racines complexes conjuguées, 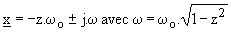; la solution générale est :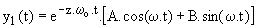

3) Solution particulière     

On applique la méthode d'identification :

Si f (t) = K = Cste , on cherche y₂ = K' = Cste; y2 = K/wo²

Si y (t) est un polynôme de degré n, on cherche un autre polynôme de degré n:

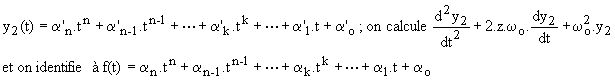
si f (t) est une fonction sinusoïdale de fréquence f, on cherche une fonction sinusoïdale de même fréquence :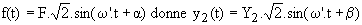

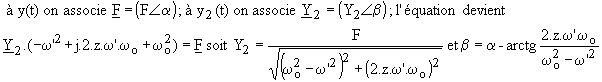
4) Solution générale

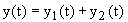
5) Calcul des constantes d'intégration

On a deux constantes A et B à calculer; pour cela on utilisera les valeurs initiales de y et dy/dt.

Le calcul étant ici assez lourd, on fera le changement de variable t' = t - t_o.

Premier cas :

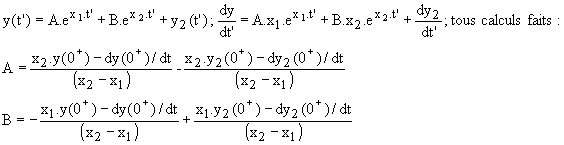
Deuxième cas :

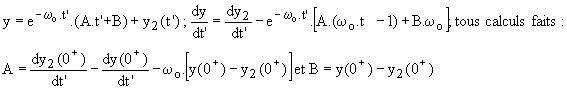
Troisième cas :

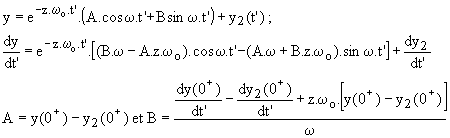
Exemple :

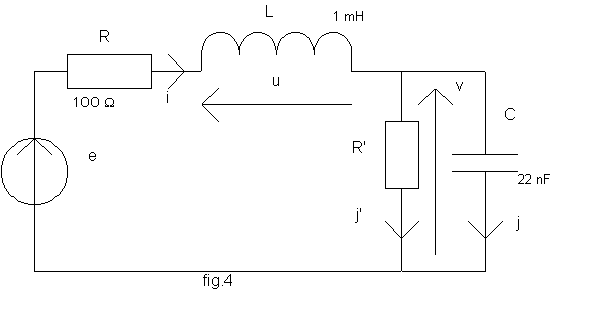
Etudions le réseau de la fig.4 : Pour t = 0^-, e = 0 ; i = 10 mA et v = 2 V. pour t > 0, .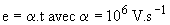

Les équations du réseau sont : i = j + j' ; (2) u = L.di/dt ; (3) j = C.dv/dt ; (4) j' = v/R' ; (5) e = R.i + u + v.

(1), (3) et (4) donnent i = C.dv/dt + v/R'. En reportant dans (2) et (5), il vient :

Prenons d'abord R' = 50 W; il vient w_o = 369 000 rd/s et z = 1,366; l'équation caractéristique a deux racines réelles x₁ = -848 000 s^-1 et x₂ = -161 000 s^-1. La solution générale de l'équation sans second membre est :

.

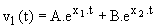Le second membre f(t) = e/L.C = a.t/LC est un polynôme du 1^er degré; nous cherchons donc une solution particulière de la forme v₂ = a.t + b. Il vient dv₂/dt = a et d²v₂/dt² = 0 d'où : 0 + 2.z.w_o.a + w_o².(a.t + b) = =a.t/LC ; nous en déduisons a = a/L.C. w_o² = 333 000 V/s et

2.z.w_o.a + w_o².b = 0 soit b = -2.z.a/w_o = -2,47 V.

Nous en déduisons la solution :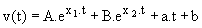

Les autres grandeurs ont pour expression :

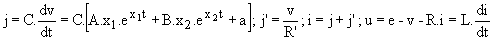
Calculons les constantes d'intégration : A t = 0⁺, les variables d'état v et i ont la valeur atteinte pour t < 0 soit v = 2 V et i = 10 mA; on en déduit j' = v/R' = 40 mA ; j = i - j' = -30 mA ; u = e - v - R.i = 0 - 2 - 1 = - 3 V. v(0) = A + B + b = 2 donne A + B = 4,47 V

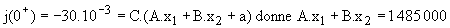; Nous en déduisons A = 1,42 V et B = 3,04 V.

La fig.5 donne l'allure des grandeurs :

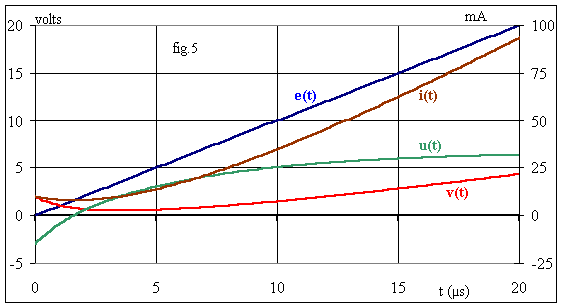
Prenons R' = 86,35 W; il vient w_o = 313 200 rd/s et z = 1; la solution générale de l'équation sans second membre est de la forme :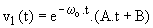

La solution particulière a la même forme que dans le premier cas, seules les valeurs numériques changent : a = 463 000 V/s et b = - 2,96 V.

La solution générale est donc de la forme :

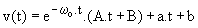
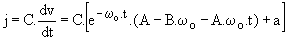
Initialement v = 2 V ; i = 10 mA ; j' = v/R' = 23,2 mA ; j = i - j' = -13,2 mA ; u = e - v - R.i = -3 V.

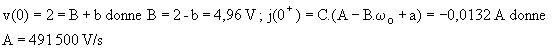
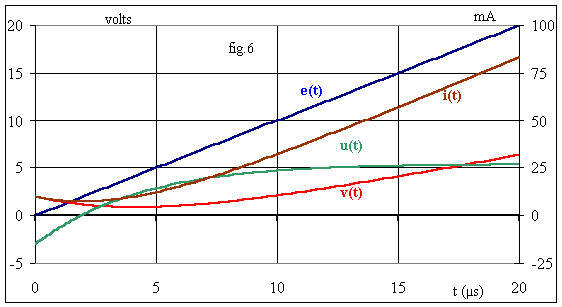
La fig.6 donne l'allure des grandeurs.

Prenons enfin R' = 500 W; il vient w_o = 233 500 rd/s et z = 0,41; la solution générale de l'équation sans second membre est de la forme :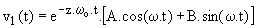

La solution particulière a la même forme que dans le premier cas, seules les valeurs numériques changent :

a = 833 000 V/s et b = - 2,92 V.

Il vient donc 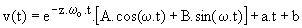avec w = 213 000 rd/s.

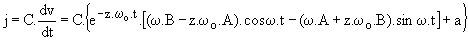
Initialement v = 2 V ; i = 10 mA ; j' = v/R' = 4 mA ; j = i - j' = 6 mA ; u = e - v - R.i = -3 V.

Nous en déduisons v(0) = A + b = 2 soit A = 4,92 V et C.(w.B-z.w_o.A+a) = 0,004 A soit B = -0,85 V.

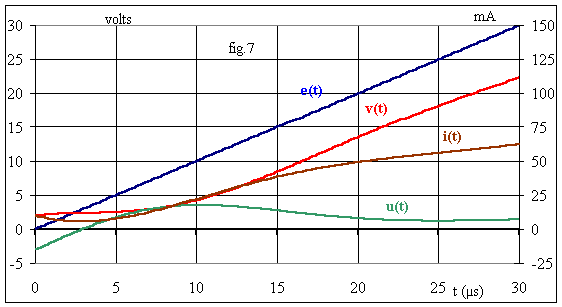
La fig.7 donne l'allure des grandeurs: