A) Échelle logarithmique

Définition

La variable de la fonction de transfert est la pulsation w ou la fréquence f. Dans de nombreuses applications, la plage de fréquences à étudier est très large, il est alors très difficile d'utiliser une échelle linéaire.

Si, par exemple, la plage va de 10 Hz à 100 kHz et si nous disposons d'une longueur de 20 cm pour tracer échelle, nous devrons adopter un coefficient d'échelle k = 100 k / 20 = 5 kHz par cm. La fréquence 10 Hz correspondra alors à un longueur L = 10 / 5000 cm = 0,002 cm = 0,02 mm ; il sera bien évidemment impossible de placer ce point sur échelle ; en admettant un précision de tracé de 0,5 mm, la fréquence la plus faible que on peut placer est 250 Hz.

Dans ce cas, il sera plus judicieux d'utiliser une échelle logarithmique : au lieu de placer la fréquence f à la longueur f/k, on la placera à abscisse L = a.log (f).

Propriétés

Le zéro d'une échelle logarithmique est rejeté en L = - ¥ . Il sera donc impossible de placer la fréquence 0.

Soit la fréquence f ' = 10.f ; sur échelle logarithmique, nous lui associons abscisse L' = a.log (10.f) soit

L' = a.(log (10) + log (f) ) = a.(1 + log (f)). L'intervalle [f ; 10.f] est appelé une décade. En échelle logarithmique, une décade est représentée par l'intervalle [L  ; L + a].

Soit la fréquence f " moyenne géométrique des fréquences f et f ' : f " = √ (f.f '). Sur l';échelle logarithmique son abscisse sera L" =a.log [√ (f.f ')] = a. [log (f) + log (f ')]/2 = (L + L')/2. Le point représentant la moyenne géométrique sera donc au milieu du segment représentant f et f '.

Construction d'une échelle logarithmique

Partant de l'intervalle de fréquences à étudier, on commence par compter le nombre de décades. Par exemple pour l'intervalle [10 Hz ; 100 kHz] on a 4 décades : 1 de 10 à 100 Hz, une de 100 Hz à 1 kHz, une de 1 kHz à 10 kHz et une de 10 à 100 kHz.

Connaissant la longueur disponible pour toute l'échelle, on définit la longueur a cm d'une décade. Par exemple pour une échelle de 20 cm et la plage ci-dessus, on aura a = 5 cm par décade.

On portera la fréquence inférieure de la première décade en L = 0 . On pourra alors porter les décades suivantes.

Repérage sur une échelle logarithmique

Soit f_i la fréquence origine de l'axe placée en L_i = 0 et a cm la longueur d'une décade.

Nous voulons placer la fréquence f₁. Nous avons f₁ = a₁.f_i soit log (f₁) = log (a₁) +log (f_i).

L'abscisse en cm est L₁ = a. log (f₁) = a.log (a₁) + L_i = a.log (a₁) car L_i = 0 par hypothèse.

Par exemple sur la fig.1 : f_i = 10 Hz et a = 5cm; si f₁ = 150 Hz, a₁ = 15 et L₁ = 5,88cm, position repérée par le trait rouge sur la figure.

Inversement si une fréquence f₂ se trouve à l'abscisse L₂, nous avons log (a₂) = L₂/a

donc 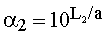et f₂ = a₂.f_i.

Par exemple, le trait bleu à l'abscisse 16,5 cm correspond à a₂ = 1995 et f₂ = 19,95 kHz

B) Définition du diagramme de Bode

Si nous voulons représenter graphiquement la fonction de transfert T (j.w) en fonction de la pulsation, nous devons tracer deux fonctions réelles de w. Le choix de ces fonctions est le gain G (w) et l';argument j (w).

Le diagramme de Bode de la fonction de transfert T (j.w) est composée de deux graphes utilisant une échelle logarithmique en abscisse :

le graphe du gain G en fonction de la pulsation ou de la fréquence

le graphe de l'argument j en fonction de la pulsation ou de la fréquence

C) Fonctions élémentaires

fonction constante réelle

T₁ = K . Le gain est G₁ = 20.log (|K|) et l'argument j₁ est égal à 0 si K ³ 0 et à 180° si K < 0.

fonction T₂ = j.w / w_o = j.f / f_o

avec f_o = w_o /2π, constante réelle positive. Pour simplifier le tracé, nous posons x = w / w_o = f / f_o ; T₂ = j.x donc

G₂ = 20log (x) et j₂ = + π/2. Le graphe du gain est une droite puisque log (x) = L, abscisse de x. Si x augmente d'une décade [x ; 10.x] , G₂ augmente de 20.log10 = 20 dB. Nous dirons que la pente de la droite est de 20 dB / décade. Cette valeur sera prise comme unité de pente dans les courbes de gain. Nous dirons donc une pente +1 pour la valeur 20 dB / décade.

La fig.2 donne le diagramme de Bode de T₂.

fonction T₃ = 1+ j.w / w_o =1+ j.f / f_o.

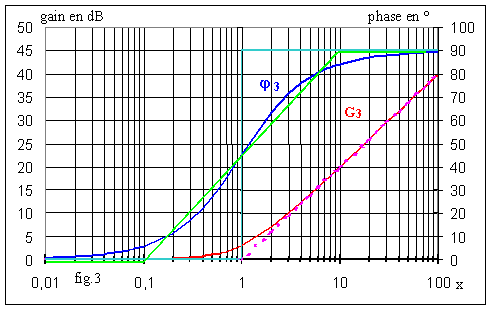
Nous posons x = w / w_o = f / f_o ; T₃ = 1+j.x donc T₃ = √ (1+x²) ; G₃ = -10log (1 + x²) et j₃ = arc tg (x) .

La fig.3 donne le diagramme de Bode :

fonction T₄ = 1+w_o / j.w =1+ f_o / j.f.

Nous posons x = w / w_o = f / f_o ; T₄ = 1+1/j.x donc T₄ = √ (1+1/x²) ; G₄ = -10.log(1+1/x²) et j₄ = -arctg(1/x) .

La fig.4 donne le diagramme de Bode:

D) Diagramme asymptotique

Le tracé exact des fonctions de transfert peut devenir lourd lorsque le degré des polynômes formant la fonction s'élève. On peut avoir une représentation approchée plus simple en se limitant à un tracé d'asymptotes.

Reprenons la fonction T₃ ; lorsque la fréquence f ® 0, x ® 0 et T₃ ® 1. Le gain et la phase tendent vers 0 ; la valeur x = 0 étant rejetée à - ¥ sur l'échelle logarithmique, l'axe des fréquences est donc l'asymptote du gain et de la phase pour x ® 0.

Lorsque f ® ¥, x ® ¥, le module T₃ = √(1+x²) est peu différent de x donc de T₂ ; la droite G₂ = 20lox (x) est donc l'asymptote du gain pour f ® ¥. j₃ = arc tg (x) : pour x ® ¥, j₃ ® π/2. Le graphe de phase de T₂ est donc l'asymptote de la phase de T₃.

Sur la fig.3 on a tracé les asymptotes, en pointillés roses pour le gain et en trait bleu clair pour la phase.

Le diagramme de Bode asymptotique de la fonction de transfert T₃ = 1+ j.f/f_o est constitué des deux demies droites asymptotes de part et d'autre de leur point d'intersection : pour f £ f_o on prend la demie droite de pente 0 passant par [f_o ; 0] et pour f > f_o on prend la demie droite de pente 20 dB/décade (soit +1) passant par [f_o ; 0] .

L'examen de la fig.3 montre que l'approximation des asymptotes donne :

un bon résultat pour le gain ; l'écart maximal entre la courbe de gain et ses asymptotes a lieu pour x = 1 ; on a alors G₃ = 20.log (√ 2) = 3 dB.

un résultat très approximatif pour la phase puisque l'écart atteint 45° au voisinage de x = 1. On peut améliorer l'approximation par le tracé en vert sur la fig.3 : on a l'asymptote f ® 0 jusqu'à x = 0,1 , l'asymptote f ®¥ pour x > 10 et on joint les deux extrémités des asymptotes par une droite. Dans ce cas l'écart avec la courbe réelle ne dépasse pas 6°.

Pour la fonction T₄, on peut utiliser la même méthode :

si x >> 1, 1/x << 1 donc T₄ » 1 ; l'asymptote du gain est la droite G₄ = 0 et celle de la phase la droite j₄ = 0.

Sur la fig.4 on a tracé en pointillés roses les asymptotes du gain et en trait bleu clair celles de la phases.

Le diagramme de Bode asymptotique de la fonction de transfert T₄ = 1+ f_o /j.f est constitué des deux demies droites asymptotes de part et d'autre de leur point d'intersection : pour f £ f_o on prend la demie droite de pente -1 passant par [f_o ; 0] et pour f > f_o on prend la demie droite de pente 0 passant par [f_o ; 0] .

Les remarques sur la précision du tracé asymptotique sont les mêmes que pour la fonction T3.