A) Enoncé

Ce théorème résulte de la linéarité des équations décrivant le fonctionnement du réseau.

Soit un réseau comportant des sources de tension de f.é.m. e₁, e₂, ..., e_k et des sources de courant i_s1, i_s2, ..., i_sp et des branches parcourues par les courants d'intensité i₁, i₂, ..., i_b.

Définissons un premier état par les valeurs de sources e₁₁, e₂₁,..., e_k1, i_s11, i_s21, ..., i_sp1. Les courants de branche ont alors les valeurs i₁₁, i₂₁, ..., i_b1.

Définissons un deuxième état par les valeurs de sources e₁₂, e₂₂, ..., e_k2, i_s12, i_s22, ..., i_sp2. Les courants de branche ont alors les valeurs i₁₂, i₂₂, ..., i_b2.

Nous dirons que nous superposons ces deux états, si nous donnons aux sources les valeurs

e₁₁+e₁₂, e₂₁+e₂₂, ..., e_k1+e_k2, i_s11+ i_s12, i_s21+ i_s22, ..., i_sp1+ i_sp2 . Les équations étant linéaires, les courants de branche dans ce nouvel état sont : i₁₁+i₁₂, i₂₁+i₂₂, .., i_b1+i_b2 .

Si nous superposons n états d'un réseau, nous obtenons des courants de branche et des tensions par dipôles égaux à la somme des grandeurs dans chacun des états.

B) Exemples

Exemple 1

On veut étudier le circuit ci-contre pour toutes les combinaisons des états ouverts et fermés des trois interrupteurs.

On donne R = 1 kW et I_s = 1 mA.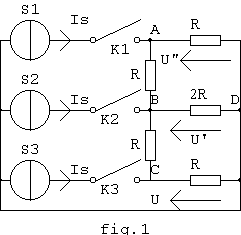

L'état Eo est celui où les trois interrupteurs sont ouverts, qui est équivalent à celui où les trois interrupteurs sont fermés et les trois courants sources sont nuls. Le réseau n'étant pas alimenté, tous les courants de branche sont nuls et U_o = 0.

L'état E1 est celui où K1 est fermé, K2 et K3 étant ouverts. Cela revient à fermer les trois interrupteurs et à donner aux courants sources les valeurs I_s, 0 , 0. Les résistances R des branches BC et CD sont en série;

V_BC = V_CD = U et V_BD = U' = 2.U. Entre B et D la résistance équivalente est 2R//2R = R. Entre A et D on a donc une résistance 2.R donc la résistance totale du circuit est R//2R = 2.R/3 et U" = 2.U'.

On a donc U" = 2.R.I_s/3 et U₁ = U'/2 = U"/4 = R.I_s/6 = 1/6 V.

L'état E2 est celui où K2 est fermé, K1 et K3 étant ouverts. Cela revient à fermer les trois interrupteurs et à donner aux courants sources les valeurs 0, I_s, 0 . Les résistances R des branches BC et CD sont en série; V_BC = V_CD = U et V_BD = U' = 2.U. De même les branches AB et AD sont en série. On a donc entre B et D trois résistances 2.R en parallèle soit une résistance équivalente 2.R/3. On a donc U' = 2.R.I_s/3 et

U₂ = U'/2 = R.I_s/3 = 1/3 V.

L'état E3 est celui où K3 est fermé, K1 et K2 étant ouverts. Cela revient à fermer les trois interrupteurs et à donner aux courants sources les valeurs 0, 0, I_s . Les branches AB et AD sont en série. On a donc entre B et D deux résistances 2.R en parallèle soit une résistance équivalente R. Cette résistance vient en série avec la branche BC. Entre C et D on a donc une résistance R//2R = 2.R/3 . On a donc U₃ = 2.R.I_s/3 = 2/3 V.

L'état E4 où K1 et K2 sont fermés et K3 ouvert est la superposition des états E1 et E2; on a donc

U₄ = U₁ + U₂ = 1/6 +1/3 = 1/2 V.

L'état E5 où K1 et K3 sont fermés et K2 ouvert est la superposition des états E1 et E3; on a donc

U₅ = U₁ + U₃ = 1/6 +2/3 = 5/6 V.

L'état E6 où K2 et K3 sont fermés et K1 ouvert est la superposition des états E2 et Ey; on a donc

U₆ = U₂ + U₃ = 1/3 +2/3 = 1 V.

L'état E7 où K1, K2 et K3 sont fermés est la superposition des états E1, E2 et E3; on a donc

U₇ = U₁ +U₂ + U₃ = 1/6 +1/3 +2/3 = 7/6 V.

Exemple 2

Etudions le circuit de la figure 2.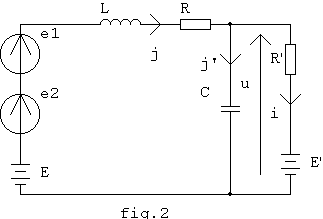

E et E' sont des sources de tension continue, e₁ est un générateur sinusoïdal de fréquence f et e₂ un générateur sinusoïdal de fréquence 3.f. On donne :

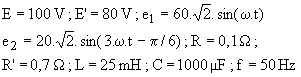
L'étude directe de ce circuit en régime permanent est difficile car on ne peut utiliser la méthode complexe avec des sources de fréquences différentes; on devrait écrire les équations en valeurs instantanées et résoudre des équations différentielles.

Définissons un état Eo où e₁ = e₂ = 0 et où on garde les sources continues.

L'état E1 est défini par E = E' = e₂ = 0 en gardant la source e₁ .

L'état E2 est défini par E = E' = e₁ = 0 en gardant la source e₂ .

La superposition de ces trois états donne à chaque source sa valeur effective et donc donne l'état réel du réseau complet.

Dans l'état Eo, en régime permanent, L est un court-circuit et C un circuit ouvert donc j'_o = 0

et i_o = j_o = (E-E')/(R+R') = 25 A et u_o = E'+R'.i_o =(R'.E+R.E')/(R+R') = 97,5 V.

Dans l'état E1, on est en régime sinusoïdal à la pulsation w = 2.π.f; on peut donc utiliser la méthode complexe.

Dans l'état E2, on est en régime sinusoïdal à la pulsation 3.w = 6.π.f; on peut donc utiliser la méthode complexe. Le calcul est formellement le même; il suffit de changer les valeurs numériques de e et de la pulsation.

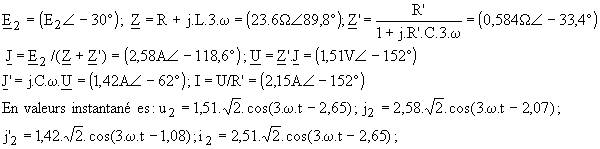
Pour connaître l'état du réseau, il suffit de superposer les trois états ci-dessus ; par exemple

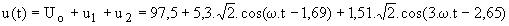
C) Types d'applications

La méthode de superposition s'applique dans les deux cas décrits par les exemples :

- toutes les sources sont de même type mais la structure du réseau peut être grandement simplifiée en éliminant une ou plusieurs sources.

- les diverses sources sont sinusoïdales de fréquences différentes; on a alors intérêt à décomposer en autant d'état qu'il y a de fréquences différentes. Dans chaque état, on peut alors appliquer la méthode complexe

Attention ! : dans ce cas il ne faut surtout pas ajouter les valeurs complexes de deux états différents mais uniquement les valeurs instantanées.