A) Addition
Reprenons la fonction a (t) et son vecteur de Fresnel  associé .
associé .
Soit une autre fonction sinusoïdale b (t) = Bmax cos (w.t+b), de même fréquence que a(t). Nous lui associons le vecteur de Fresnel 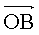 défini par sa norme
défini par sa norme 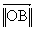 = B = Bmax /√2 et son angle polaire b.
= B = Bmax /√2 et son angle polaire b.
Construisons par la règle du parallélogramme, le vecteur 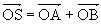 .
.
Projetons orthogonalement sur Ox’ les trois vecteurs respectivement en a, b et s. Le théorème des projections implique 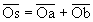 soit s(t) /√2 = [a (t)+b (t)]/√2. Le vecteur
soit s(t) /√2 = [a (t)+b (t)]/√2. Le vecteur 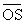 est donc le vecteur de Fresnel associé à la somme s (t) des fonctions a et b. Nous en déduisons graphiquement la valeur efficace
est donc le vecteur de Fresnel associé à la somme s (t) des fonctions a et b. Nous en déduisons graphiquement la valeur efficace
S =  et la phase à l’origine
et la phase à l’origine 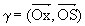 . Nous pouvons alors écrire : s(t) = a(t) + b (t) = S.√2.cos (w.t+g).
. Nous pouvons alors écrire : s(t) = a(t) + b (t) = S.√2.cos (w.t+g).
La méthode des vecteurs de Fresnel permet donc de calculer simplement la somme de deux fonctions sinusoïdales de même fréquence.
Pour nous affranchir de l'imprécision due à la construction graphique, nous pouvons utiliser les relations suivantes dans un triangle quelconque représenté fig.3 :
En appliquant par exemple ces relations au triangle ABS de la fig.2, il vient :
Attention ! : nous constatons que dans le cas général,
les valeur efficaces ne s'ajoutent pas ; nous pouvons seulement dire à priori que
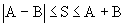
.
B) Dérivation
Soit a’(t) = da /dt la fonction dérivée de a(t). Nous avons a' = -w.Amax sin (w.T+α) soit
a' (t) = w.Amax cos (w.t + a +π/2). La fonction dérivée a donc pour valeur efficace A' = w.A et pour phase à l'origine a'= a +π/2. Si nous lui associons le vecteur de Fresnel , nous obtenons le graphe de la fig.4.
Nous pouvons dire que le vecteur de Fresnel associé à la dérivée a' se déduit de celui associé à la fonction par :
rotation de + π /2
homothétie de centre O et de rapport w (multiplication du module par w) C) Intégration
Soit p(t) la fonction primitive de a(t) et son vecteur de Fresnel associé. Nous avons a = dp/dt. Nous savons donc déduire le vecteur de Fresnel associé à p(t) par la règle du paragraphe 3.2 (fig.5).
Nous pouvons dire que le vecteur de Fresnel associé à la primitive p se déduit de celui associé à la fonction par :
rotation de -π/2
homothétie de centre O et de rapport 1/w (division du module par w ).
D) Exemple
Soit trois fonctions sinusoïdales de même pulsation w = 2 rd/s :
a (t) = 20√2.cos (2.t+5π/6) ; b (t) = 10√2.sin (2.t) ; c(t) = 5√2.cos (2.t-3π/4).
Nous voulons calculer la fonction d(t) = 2.π (t) +1,5.b (t) - 2,5.dc /dt, p étant la fonction primitive de a.
Construisons fig.6 les vecteurs de Fresnel :
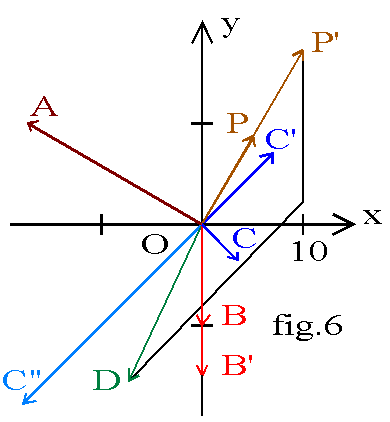
 associé à a (t) défini par OA = 20 et (Ox,OA) = + 5P/6
associé à a (t) défini par OA = 20 et (Ox,OA) = + 5P/6
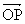 associé à p(t) défini par OP = OA/ w = 10 et (Ox,OP) = +5p/6-π/2 = + π/3
associé à p(t) défini par OP = OA/ w = 10 et (Ox,OP) = +5p/6-π/2 = + π/3
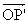 associé à 2.π(t) défini par
associé à 2.π(t) défini par 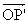 = 2.
= 2. 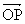
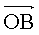 associé à b (t) = 10√2.sin (2.t) = 10√2.cos (2.t - π/2) défini par OB = 10 et (Ox,OB) = -π/2
associé à b (t) = 10√2.sin (2.t) = 10√2.cos (2.t - π/2) défini par OB = 10 et (Ox,OB) = -π/2
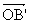 associé à 1,5.b (t) soit
associé à 1,5.b (t) soit 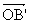 = 1,5.
= 1,5.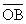
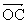 associé à c (t) défini par OC = 5 et (Ox,OC) = -3π/4
associé à c (t) défini par OC = 5 et (Ox,OC) = -3π/4
 associé à c’(t)= dc /dt défini par OC’ = w.OC = 10 et (Ox,OC’) = π/2-3π/4 = 3π/4
associé à c’(t)= dc /dt défini par OC’ = w.OC = 10 et (Ox,OC’) = π/2-3π/4 = 3π/4
 associé à -2,5.dc/dt soit
associé à -2,5.dc/dt soit  = -2,5.
= -2,5. 
Traçons le vecteur somme 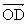 associé à la fonction d (t). La longueur OD donne la valeur efficace D = 17 et l’angle (Ox,OD) donne la phase à l’origine d = -2 rd.
associé à la fonction d (t). La longueur OD donne la valeur efficace D = 17 et l’angle (Ox,OD) donne la phase à l’origine d = -2 rd.
Nous pouvons donc écrire d(t) = 17√.2cos (2.t - 2).

