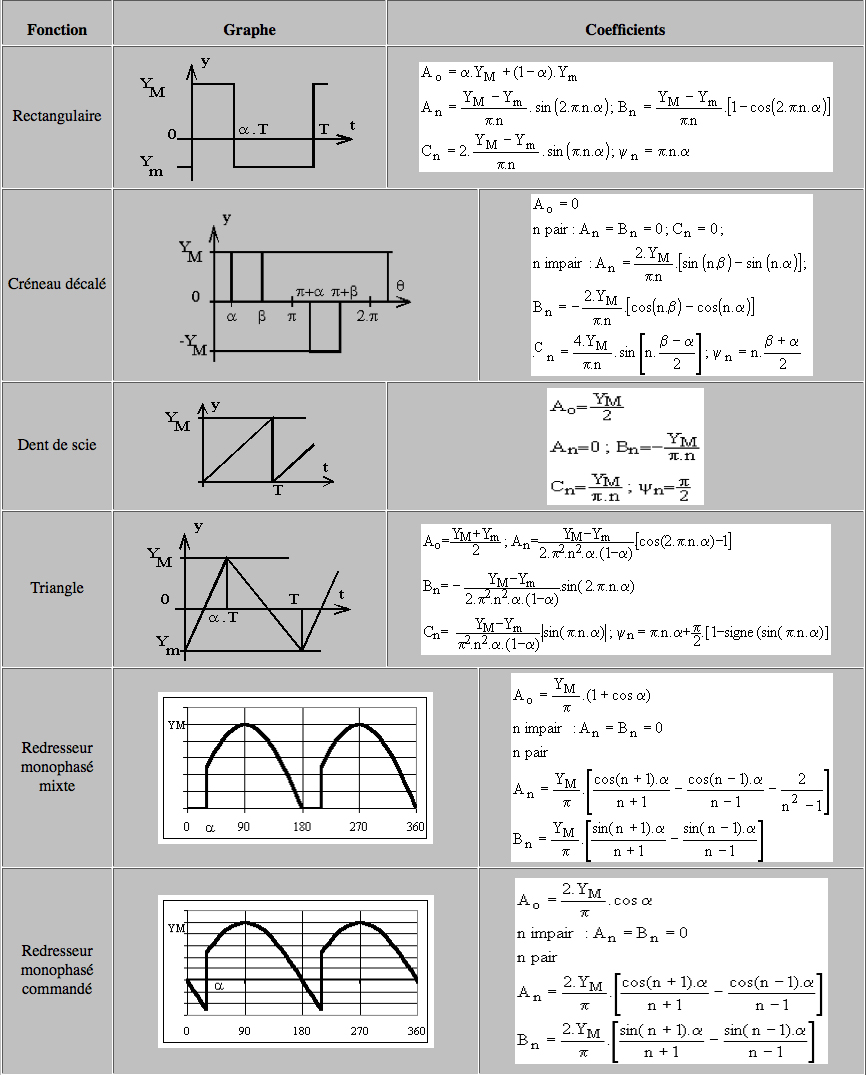
A) Théorème de Fourier
Toute fonction périodique de fréquence f, peut être décomposée en la somme d'un terme constant et de termes sinusoïdaux de fréquences f, 2.f, 3.f, ..., n.f
L'écriture de la série peut prendre deux formes :
Le terme de fréquence f est appelé harmonique de rang 1 ou fondamental ; le terme de fréquence n.f est appelé harmonique de rang n ou en abrégé harmonique n.
B) Calcul des coefficients
Remarques préliminaires
Remarque 1 : Toute fonction alternative est de valeur moyenne nulle sur une période.
Remarque 2 : Calculons la valeur moyenne de cos (n.θ).cos (m.θ) avec θ = w.t sur une période [0 ; 2π]:
La valeur moyenne de cos(n.θ).cos(m.θ) est donc égale à 0 si n ¹ m et à 1/2 si n = m. Il en est de même pour sin(n.θ).sin(m.θ). On peut montrer de même que la valeur moyenne de cos(n.θ).sin(m.θ) est nulle dans tous les cas.
C) Valeur des coefficients
Calculons la valeur moyenne de y (t) sous la première forme :
D'après la remarque 1, il vient Yo = Ymoy.
Calculons la valeur moyenne de y (t).cos (n.w.t):
D'après la remarque 1, le premier terme est de valeur moyenne nulle ; d'après la remarque 2, le deuxième terme a pour valeur moyenne 0 si n ¹ m et 1/2 si n = m ; le troisième terme est de valeur moyenne nulle. Il vient donc :
Calculons la valeur moyenne de y (t).sin (n.w.t) :
D'après la remarque 1, le premier terme est de valeur moyenne nulle ; d'après la remarque 2, le deuxième terme est de valeur moyenne nulle, le troisième terme a pour valeur moyenne 0 si n ¹ m et 1/2 si n = m ; le troisième terme. Il vient donc :
Calculons les coefficients de la deuxième forme :

D) Influence des symétries de la fonction
Si une fonction présente des symétries, tous les termes de la série de Fourier doivent présenter les mêmes symétries. Tout terme n'ayant pas les mêmes symétries que la fonction doit s'annuler par annulation du coefficient An ou Bn.
Les symétries possibles sont :
fonction paire = symétrie par rapport à l'axe Oy ; y (-t) = y (t); cos (n.w.t) est une fonction paire alors que sin (n.w.t) est impaire ; dans ce cas, tous les coefficients Bn sont nuls.
fonction impaire = symétrie par rapport à l'origine O ; y (-t) = -y (t); cos (n.w.t) est une fonction paire alors que sin (n.w.t) est impaire ; dans ce cas, tous les coefficients An sont nuls.
fonction alternative : symétrie par rapport au point (T/2 ; 0); y (t+T/2) = -y (t).
Si n est pair, n = 2π : cos [2π.(w.t + p)] = cos(2π.w.t + 2π.p) = cos (2π.w.t) ,
sin [2π.(w.t + p)] = sin(2π.w.t + 2π.p) = sin (2π.w.t
si n est impair, n = 2π+1 :
cos [(2π+1).(w.t + p)] = cos[(2π+1).w.t + 2π.p + p] = cos [(2π + 1).w.t + p] = - cos [(2π + 1).w]
sin [(2π + 1).(w.t + p)] = sin [(2π + 1).w.t + 2π.p + p] = sin [(2π + 1).w.t + p] = - sin [(2π + 1).w].
Seuls les harmoniques de rang impair sont alternatifs ; dans ce cas, tous les harmoniques de rang pair sont nuls : A2p = B2p = 0.
fonction "redressée" : symétrie par rapport à l'axe t = T / 2 : y (t + T/2) = y (t).
Seuls les harmoniques de rang pair ont la même symétrie ; dans ce cas, tous les harmoniques de rang impair sont nuls : A2p+1 = B2p+1 = 0.
La présence de symétrie limite le nombre des coefficients à calculer ; il est important de rechercher ces symétries avant de débuter le calcul.
Il est parfois possible de faire apparaître des symétries par changement de variable
èen ajoutant une constante à la fonction : y' (t) = y (t) + K a les mêmes coefficients An et Bn que y (t) et Y'o = Yo + K.
Par exemple la fonction la fonction y (t) de la fig.1 ne présente aucune symétrie.
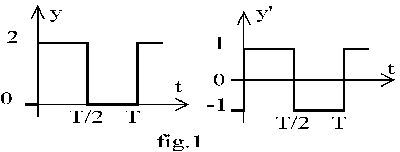
La fonction y' (t) = y (t) -1 est impaire et alternative donc il suffit de calculer les coefficients B2p+1.
En faisant un changement de variable t' = t - to.
Sur la fig.2, la fonction y est alternative mais ni paire ni impaire
En faisant le changement de variable : q' = θ - (p + a)/2, la fonction devient paire ; il suffit donc de calculer les coefficients A2p+1.
Décomposition en série de Fourier des fonctions usuelles :