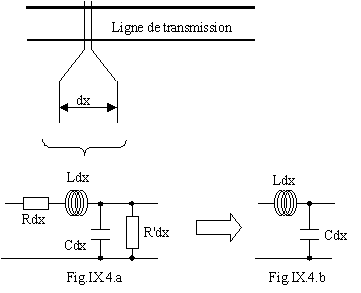
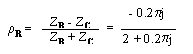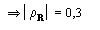Une ligne de transmission peut
être assimilée à une mise en cascade de cellules élémentaires de dimension dx
infinitésimale, constituées d'une self infinitésimale L.dx, d'un condensateur C.dx,
d'une résistance R.dx et d'une résistance de fuite R'.dx (fig.IX.4.a).
Si la longueur de la ligne n'est pas trop grande, les éléments
R.dx et R'.dx peuvent être négligés, ce qui permet de simplifier le modèle
mathématique (fig.IX.4.b).
On parlera alors de ligne sans pertes.
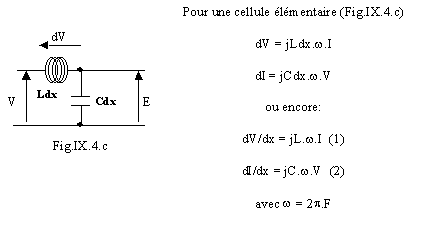
En dérivant l'équation (1) par rapport à x, il vient:
d2V/dx2
= jLw.dI/dx
en remplaçant dI/dx par sa valeur
dans l'équation (2)
d2V/dx2
+
LCw2
.V = 0
En dérivant
(2) et en remplaçant dV/dx par sa valeur dans l'équation (1), il vient:
d2I/dx2 + LCw2 .I = 0
Ces deux équations différentielles du 2ème
ordre, appelées équations des télégraphistes,
caractérisent les variations en tension et en courant,
en fonction de la distance x,
sur une ligne de transmission sans pertes.
Du quotient des deux équations (1) et (2) il vient
dV/dI =
(L/C).(
I
/ V ) Û
V.dV = (L/C). I.dI en intégrant
ò
V.dV = (L/C). ò
I.dI
Þ V/I = Ö(L/C) = Zc
Zc impédance caractéristique de la ligne est une grandeur réelle
Zc =
Ö(L/C)
Les solutions des équations différentielles du 2ème
ordre s'écrivent:
V(x)
= K1.e-jbx + K2.ejbx
I(x) = C1.e-jbx +
C2.ejbx
K1, K2,C1
et C2 sont des constantes d'intégration arbitraires
déterminées par les conditions
aux limites (générateur et charge).
b
= w.ÖLC
est appelé constante de
propagation
Ces deux équations traduisent la
superposition sur la ligne
d'une onde incidente et
d'une onde réfléchie de sens opposés.
Les formules d'Euler permettent
d'écrire:
V(x)
= VR . [cosbx + j(ZC/ZR).sinbx]
I(x) = IR . [cosbx + j(ZR/ZC).sinbx]
Ou encore
V(x) = (IR/2). [(ZR – ZC).e-jbx + (ZR + ZC).e
jbx]
I(x) = (IR/2ZC). [(ZR – ZC).e-jbx + (ZR + ZC).e
jbx]
Ces
équations expriment les valeurs de la tension et du courant,
en un point quelconque x de la ligne, en prenant comme origine
le récepteur (Fig.IX.5).
Les termes en e-jbx représentent
l'onde réfléchie et les termes en e jbx,
l'onde incidente.
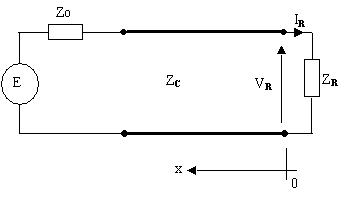
Fig. IX.5
On appelle coefficient de
réflexion r, le rapport
onde réfléchie / onde incidente.
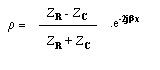
En
particulier sur la charge (x = 0)
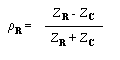
La charge ZR est
la plupart du temps une grandeur complexe.
Si ZR = ZC
la ligne est adaptée rR =
0
il n'y a pas de réflexions et
toute l'énergie émise est absorbée par la charge.
Si ZR = 0
(court-circuit) Þ rR =
-1
l'onde réfléchie a la même
amplitude que l'onde incidente,
mais elle est en opposition de
phase.
Si ZR = µ (ligne
ouverte) Þ rR =
+1
l'onde réfléchie est en phase
avec l'onde incidente et est de même amplitude.
Puisque ZR est
la plupart du temps une impédance complexe et ZC une impédance
réelle, il est rarement possible d'adapter parfaitement la ligne et l'objectif est alors
de minimiser au mieux les réflexions.
Si
l'on introduit les pertes (qui ont été négligées jusqu'à maintenant), une onde sinusoïdale se propageant sur la ligne, s'atténuera de façon
exponentielle avec la distance. (Fig. 9.2.e)
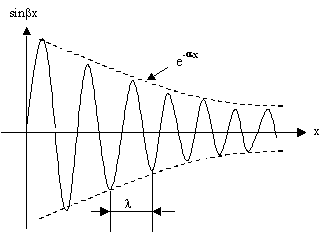
Fig. IX.6 Atténuation dans
l'espace
Puisque bx augmente de 2p lorsque x
augmente de l il vient:
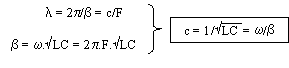
La vitesse de propagation sur une
ligne de transmission dépend
des caractéristiques physiques de
cette ligne.
Pour un câble coaxial de rayon r1
= 1,29mm et r2 = 4,7mm (Fig.IX.7)
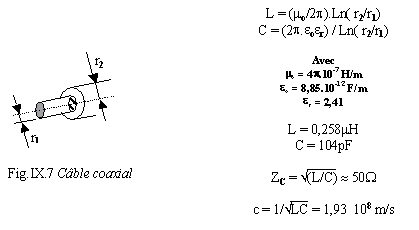
Si une ligne d'impédance
caractéristique ZC est connectée à une charge ZR ¹ ZC,
le coefficient de réflexion rR
est différent de zéro, ce qui se traduit par la propagation simultanée d'une onde
incidente et d'une onde réfléchie.
Il se crée dès lors, un système
d'ondes stationnaires sur la ligne.
V(x)
= VR . [cosbx + j(ZC/ZR).sinbx]
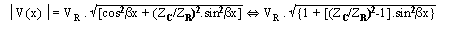
sin2bx = 0 Þ½V(x)
½max
= VR
sin2bx = 1 Þ½V(x)
½min
= VR . ZC/ZR
Le Taux d'Ondes Stationnaires TOS
est défini par:
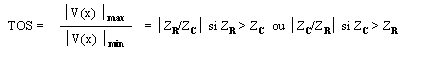
Si ZR
est une impédance réelle purement résistive alors:
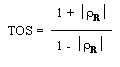
1 = TOS < µ
Une ligne adaptée se traduit par un coefficient de réflexion rR = 0
Þ
TOS = 1.
Tos mètre

Un
TOS compris entre un et trois est considéré comme acceptable, dans la plupart des
applications.
Pour
l'onde réfléchie, la charge se comporte dès lors comme un émetteur et l'émetteur
devient un récepteur.
Il apparaît à l'entrée de la
ligne, un coefficient de réflexion sur le générateur:
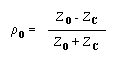
Puissance
absorbée par la charge est donnée par:
P = Pi ( 1 - ½rR½2)
Pi =
puissance incidente
Application numérique:
Supposons
un émetteur radio de fréquence porteuse F = 100MHz, de puissance 100W, (Fig. IX.8)
relié par l'intermédiaire d'un câble coaxial (Fig.IX.7) à une charge, constituée
d'une résistance R en parallèle avec un condensateur C.
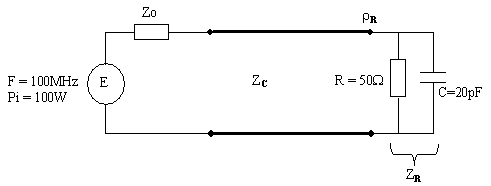
Fig. IX.8 Ligne chargée par un
circuit RC parallèle
L'impédance caractéristique de
la ligne est:
ZC
=
Ö(L/C)
»
50W
La vitesse
de propagation:
w
= 2p.F = 2p.108
rd/s
c = 1/ÖLC
= 1,93 . 108 m/s
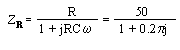
Le
coefficient de réflexion sur la charge est: