Exercice
1
Lors
d'un orage, un observateur mesure le temps t séparant l'éclair du tonnerre.
Quelle
distance sépare l'observateur du point d'impact de la foudre lorsque t = 10s ?
La
vitesse du son cSon dans l'air est supposée égale à 343m/s.
La
vitesse de la lumière cLum est, quant à elle, égale à 3.108m/s.
La
vitesse de la lumière étant très supérieure à la vitesse du son, on peut négliger le
temps mis par la lumière pour atteindre l'observateur.
La
distance x parcourue par le son pendant le temps t = 10s est:
x = cSon.t
x =
343.10 = 3,43km
Le temps mis par la lumière pour parcourir cette
distance est:
tL
= x / cLum = 3430/(3.108) = 11,43ms
L'erreur sur la distance est donc égale à:
Dx
= cSon.tL » 4mm !
Exercice 2
Un dispositif de mesure à ultrasons (télémètre ultrasonore)
est équipé d'un transducteur émetteur E et d'un transducteur récepteur R.
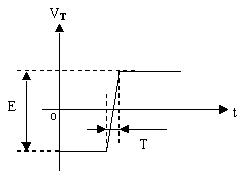
Le signal émis est constitué de trains d'ondes sinusoïdales de
fréquence F = 40kHz, de durée
t
= 100ms et de période
de répétition To = 100ms.
Le dispositif électronique, associé à ces transducteurs, permet
la mesure du temps tR séparant l'envoi d'un train d'ondes ultrasonores
de son écho issu d'une surface plane.
La vitesse de propagation c des
ultrasons dans l'air est supposée égale à 340m/s.
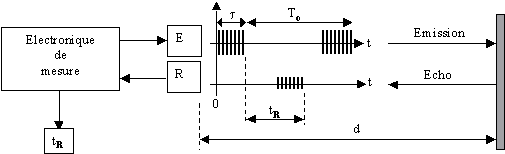
Questions:
a) De
combien de périodes de sinusoïdes est constitué chaque train d'ondes ?
b)
Quelle est la distance maximale de mesure dMaxi de ce télémètre ?
c)
Quelle est la distance minimale de mesure dMini de ce télémètre ?
d) A
quelle distance d correspond à un temps de retour tR = 30ms ?
Réponses:
a) La
fréquence F des ondes ultrasonores sinusoïdales est égale à 40kHz.
La période de ces signaux est donc égale à:
T = 1/F = 25ms
Le nombre de sinusoïdes comprises dans une impulsion de
durée t = 100ms est:
N = t / T = 4
b) La
distance maximale de mesure est fonction de la période de répétition des trains
d'ondes.
dMaxi = c.To/2 =
340.50 10-3 = 17m
c) La
distance minimale de mesure est fonction de la durée
t des trains
d'ondes.
dMini =
c. t/2 = 170.10-4
= 1,7cm
dMini = Dd = 1,7cm est le plus petit intervalle de distance
mesurable
d) Un
temps de retour tR = 30ms correspond à une distance d égale à:
d = c. tR/2 = 340.15 10-3
= 5,1m
Exercice 3
Un radar Doppler de contrôle de vitesse automobile, de fréquence
F = 24,125GHz (Mesta 208 bande K), émet des trains d'ondes avec une PRF (Pulse Repetition
Frequency) F0 = 30kHz.
L'angle Doppler a entre l'axe du
faisceau radar et l'axe de déplacement des véhicules mesurés est égal à 25°.
Questions:
a) Quelle est la longueur d'onde du signal émis ?
b) Quelle est la vitesse maximale ôVMaxi
ômesurable par
ce radar ?
c) A quelle fréquence Doppler DF correspond une
vitesse mesurée égale à 130km/h ?
d) Le calcul de la vitesse est réalisé au moyen d'un algorithme
de FFT sur un nombre N = 256 points. Quelle est la précision dv sur la mesure de la
vitesse ?
Réponses:
a) Longueur d'onde l
l
= c/F = 3.108 / 24,125 109 = 1,24cm
b) La
vitesse maximale mesurable est proportionnelle à la PRF.
ôVMaxi
ô= (l/4).F0
= (1,24/4).10-2 .3.104 = 93m/s = 334km/h
c) Une
vitesse v = 130km/h = 36,11m/s correspond à une fréquence Doppler égale à:
DF = (2.v/l). cosa
a
= 25° Þ cosa = 0,906
DF
= 0,906.7222/1,24 = 5277Hz
d) La
précision sur la mesure de la vitesse est fonction du nombre de points de la FFT.
dv = (l.F0)
/ 2.N = 372/512 = 0,726m/s = 2,6km/h
La durée d'une mesure est égale à N/Fo
= 256/(3.104) = 8,5ms
(Pendant cette mesure le véhicule circulant à 130km/h
se déplace de 30cm)
Exercice 4
Un
radar aérien Doppler de contrôle d'approche émet une OEM de fréquence F = 3GHz
La
durée t
des impulsions émises est égale à 1ms
et la période de répétition T0 est de 100ms.
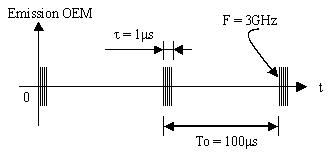
Questions:
a) Quelle est la longueur d'onde du signal émis ? Que vaut la PRF
?
b) Quelle est la vitesse maximale ambiguëôVMaxi
ômesurable par
ce radar ?
c) Quelle est la distance maximale de mesure dMaxi
?
d) Quelle est la zone aveugle de ce radar ?
e) Deux avions, en cours d'atterrissage, se suivent avec un
écartement de 120m.
Que voit le contrôleur aérien sur son écran radar ? Pourquoi ?
Réponses:
a)
Longueur d'onde et PRF.
l
= c/F = 3.108 / 3.109 = 10cm
La PRF F0 est égale à:
F0 = 1/T0 = 10kHz
b) La
vitesse maximale mesurable est proportionnelle à la PRF.
ôVMaxi ô= (l/4).F0 = 900km/h
c) La
distance maximale de mesure est inversement proportionnelle à la PRF
dMaxi =
c / (2.F0) = 1,5.104 = 15km
d) La
zone aveugle du radar est fonction de la durée des impulsions électromagnétiques.
Zone aveugle = c. t/2 = 150m
e) Le
radar ne peut distinguer deux échos qui ne seraient pas espacés dans le temps de la
durée t. Cet
intervalle définit la résolution radiale Dd.
Dd
= c. t/2 = 150m
Les
deux avions étant alignés sur le même axe du faisceau radar et écartés de seulement
120m, le contrôleur aérien ne verra donc qu'un seul plot sur son écran au lieu de deux.
Exercice
5
Un radar météorologique en bande
S (F = 2,9GHz) émet des impulsions électromagnétiques de durée
t
= 4ms
avec une PRF F0 = 1kHz.
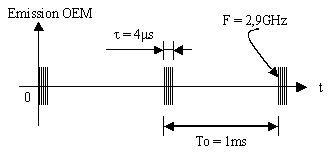
Questions:
a) Quelle est la longueur d'onde du signal émis ?
b) Quelle est la vitesse Nyquist ôVMaxi
ômesurable par
ce radar ?
c) Quelle est la distance maximale de mesure dMaxi
?
d) Quelle est la zone aveugle de ce radar ?
e) Compte tenu de la rotondité terrestre, quelle est la hauteur
par rapport au sol, atteinte par le faisceau radar à la distance maximale de mesure ?
Réponses:
a) La
longueur d'onde est égale à:
l
= c/F = 3.108 / 2,9.109 = 10,4cm
b) La
vitesse de Nyquist mesurable est:
ôVMaxi
ô= (l/4).F0
= 26m/s
c) La
distance maximale de mesure est:
dMaxi =
c / (2.F0) = 3.108 / 2.103 = 1,5.105
= 150km
d) La
zone aveugle du radar est:
Zone aveugle = c. t/2 = 600m
e) La hauteur, par rapport au sol, atteinte par le
faisceau radar, à la distance dMaxi est égale à:
h = (dMaxi)2 /
2R
avec R le rayon moyen de la terre
= 6370km
h = 1766m
Exercice 6
Un radar Doppler OEM de fréquence F = 21GHz, placé sur le
central de Roland Garos enregistre une variation de fréquence DF = 7kHz lors
du service de Gustavo Kuerten.
L'angle de visée Doppler a est égal à
20°. La PRF Fo est égale à 20kHz.
Questions:
a)
Quelle est la vitesse maximale mesurable par ce radar?
b)
Quelle est la vitesse de la balle de Guga?
Réponses:
a)
l = c/F = 3.108
/ 21.109 = 1,4cm
ôVMaxi ô= (l/4).F0 = 71,4m/s = 257km/h
b)
DF = (2.v/l). cosa Þ v = l.DF/(2.cosa)
a = 20° Þ cosa = 0,94
v = 52,1 m/s =
187,6km/h
Exercice 7
Un
véhicule circulant en agglomération (vitesse limitée à 50km/h) est contrôlé par un
radar Doppler de la gendarmerie de type Mesta 208, bande K (F = 24,125GHz). Au passage du
véhicule l'onde écho est de fréquence F' = F + 2500Hz.
L'angle
de visée est égal à a = 25°.
Question:
ce véhicule est-il en infraction ?
Réponse:
Oui
F = 24,125GHz Þ l = 1,24cm
DF = 2500Hz
cosa = 0,906
v = l.DF/(2.cosa) = 17,1m/s = 61,6km/h !
Un navire est équipé d'un sonar de bathymétrie qui émet des
impulsions ultrasonores de fréquence F = 50kHz avec une périodicité T0
= 3s.
La vitesse de propagation c des
ultrasons dans l'eau de mer est supposée égale à 1500m/s
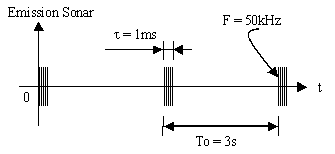
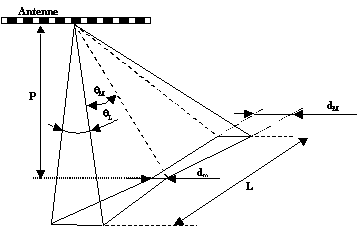
To = 2.P/ (c.cosqM) Þ P = (To.c.cosqM)/2
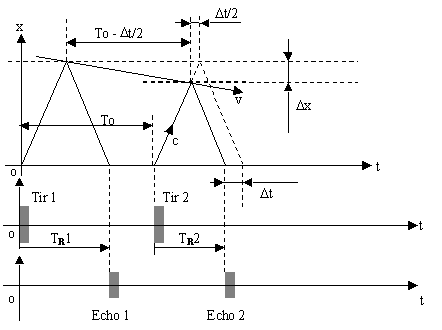
Echographie CVI ( Color Velocity Imaging)
En
échographie CVI, la vitesse d'une cible n'est pas obtenue par effet Doppler mais en
calculant l'écart Dt entre deux
échos successifs.
La
vitesse de la cible est supposée constante pendant la mesure.
L'angle
Doppler a est connu et
égal à 20°.
La
profondeur maximale d'exploration est fixée à 20cm.
La
vitesse de propagation c des ultrasons dans le milieu est égale à 1540m/s.
Questions:
a)
Quelle est la PRF dans ce cas?
b) Calculer
Dt
pour une vitesse v de cible égale à 1m/s ?
Caractéristiques
acoustiques d'un matériau piézo-électrique

c = ZT / r = 3696m/s
e = c / (2.F) Þ F = c/(2.e) = 721,8kHz