Mesures de symétrie
Introduction
Pour comprendre la notion de symétrie et d'asymétrie, il faut faire appel aux représentations graphiques (ici, le diagramme en bâtons).
Une distribution de valeurs peut être symétrique, asymétrique à gauche, asymétrique à droite.
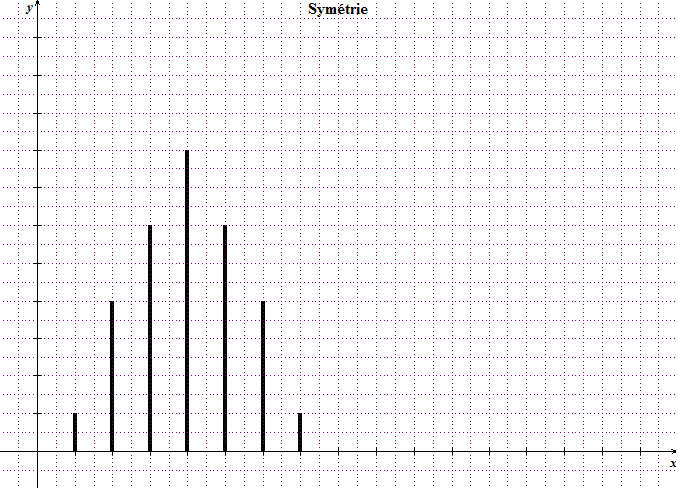
Dans ce cas on constate en général que la moyenne est égale à la médiane et aussi au mode.
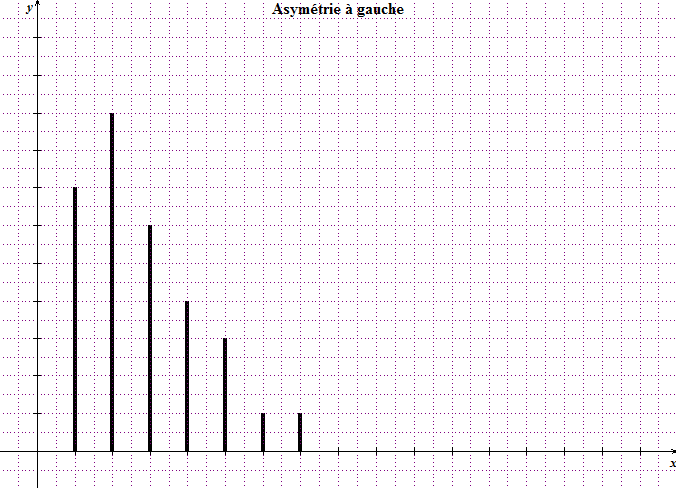
Dans ce cas on constate généralement que la moyenne est supérieure à la médiane qui elle-même est supérieure au mode.
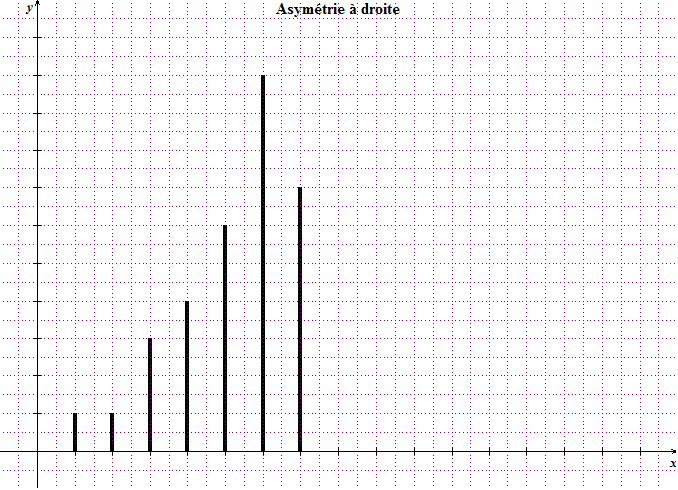
Dans ce cas on constate généralement que la moyenne est inférieure à la médiane qui elle-même est inférieure au mode.
Il peut être utile de quantifier l'asymétrie et non pas seulement de la constater.
C'est l'objet de ce qui suit.
Les moments centrés
Quand on connait les valeurs de la série statistique, on peut définir les moments centrés.
Le moment centré d'ordre p est :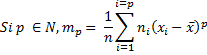 
Nous connaissons le moment centré d'ordre 1 :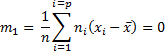 
Nous connaissons aussi le moment centré d'ordre 2 :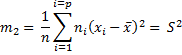 
, c'est la variance.
Pour quantifier l'asymétrie, nous utiliserons le moment centré d'ordre 3 :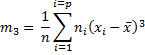 
.
Le moment centré d'ordre 3 est nul si la distribution est symétrique ( à chaque écart à la moyenne positif correspond son symétrique négatif, et l'élévation au cube conserve le signe).
On montre facilement que si la distribution est asymétrique à gauche, le moment centré d'ordre 3 est positif.
De même, si la distribution est asymétrique à droite, le moment centré d'ordre 3 est négatif.
Le signe du moment centré d'ordre 3 indique donc le sens de l'asymétrie.
Mais nous voulions quantifier l'asymétrie... et le simple fait de changer d'unité fait varier les moments de façon considérable...Il faudrait trouver un nombre sans dimension (sans unité) pour la quantifier. C'est l'objet du paragraphe qui suit...
Le coefficient d'asymétrie de Fischer
Il permet de déterminer le sens de l'asymétrie et de quantifier sa valeur.
"Gamma 1" est le quotient du moment centré d'ordre 3 par le cube de l'écart type.
Le signe de "gamma 1" est donc égal à celui du moment centré d'ordre 3 car l'écart -type est positif.
Numérateur et dénominateur s'expriment avec une unité qui est le cube de l'unité de la variable. Le quotient est donc sans unité : c'est ce que nous voulions.
Gamma 1 est nul si la distribution est symétrique .
Si la distribution est asymétrique à gauche, Gamma 1 est positif.
Si la distribution est asymétrique à droite, Gamma 1 est négatif.
Le signe de Gamma 1 indique donc le sens de l'asymétrie.
De plus, si Gamma 1 augmente en valeur absolue, cela veut dire que la distribution devient de plus en plus asymétrique.
Les coefficients empiriques
Ce sont des coefficients plus faciles à calculer que le coefficient d'asymétrie de Fischer, mais ils ne sont pas justifiables mathématiquement.
Il est possible que ces coefficients, lorsque l'asymétrie n'est pas trop marquée, donnent des résultats différents.
Le coefficient empirique de Pearson
C'est le nombre sans unité :
Il possède les mêmes propriétés que le coefficient d'asymétrie de Fischer :
Sk est nul si la distribution est symétrique .
Si la distribution est asymétrique à gauche, Sk est positif.
Si la distribution est asymétrique à droite, Sk est négatif.
Le signe de Sk indique donc le sens de l'asymétrie.
Le coefficient empirique de Yule et kendall
C'est le nombre sans unité :
Il possède les mêmes propriétés que le coefficient d'asymétrie de Fischer :
Yk est nul si la distribution est symétrique .
Si la distribution est asymétrique à gauche, Yk est positif.
Si la distribution est asymétrique à droite, Yk est négatif.
Le signe de Yk indique donc le sens de l'asymétrie.
Il est immédiat que Yk est compris entre -1 et 1.