Pour comprendre les mesures d'applatissement, on peut faire appel à des représentations graphiques :

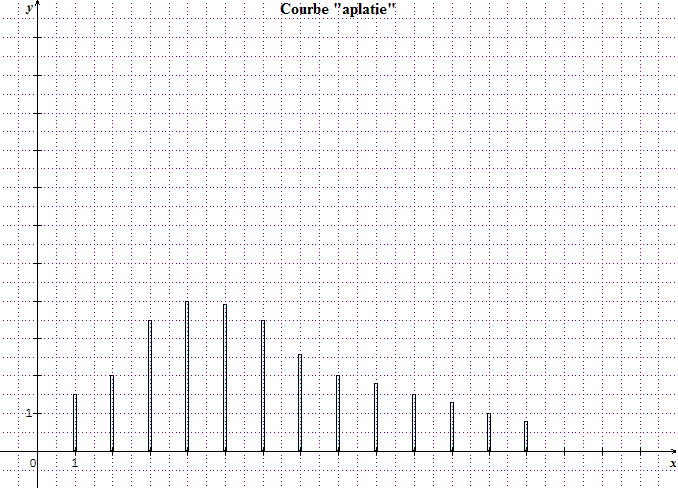
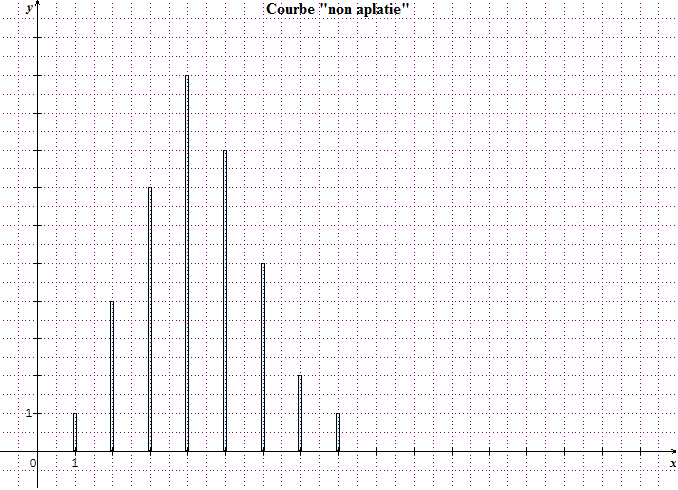
Si la loi est continue :

 

 

 

 

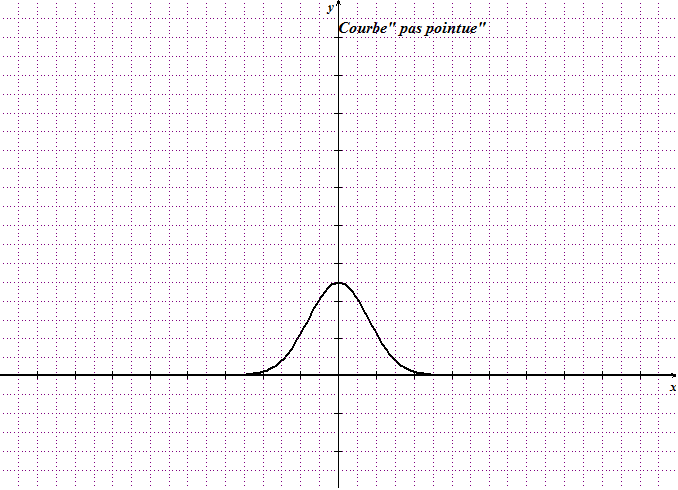
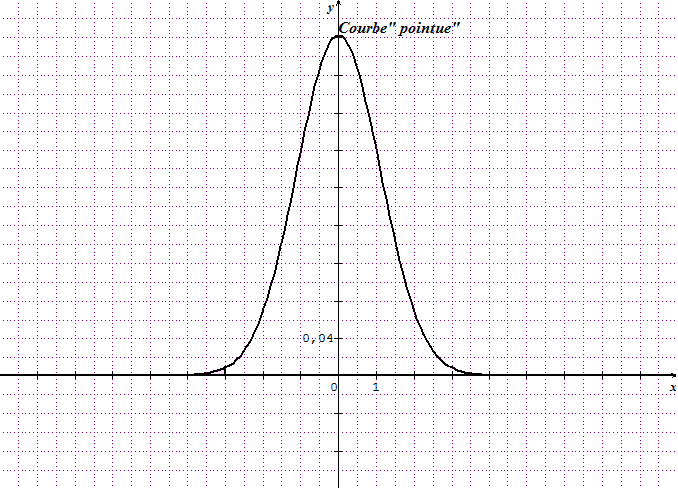
Il peut être utile de quantifier l'aplatissement et non pas seulement de le constater.

C'est l'objet de ce qui suit. 

 

C'est le nombre sans dimension égal à :

, où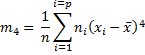

m₄ est le moment centré d'ordre 4 de la distribution.

Si le coefficient d'aplatissement de Pearson est  "grand", la courbe est "pointue".

Pour une loi Normale, le coefficient d'aplatissement de Pearson est égal à 3.

On définit alors le coefficient d'aplatissement de Fischer  :

Le coefficient de Fischer permet de  situer l'aplatissement par rapport à une loi Normale.