L'hypothèse alternative H1 est alors le contraire de H0.

Cette hypothèse alternative consiste alors à dire que 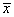et 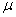sont trop éloignées l'une de l'autre pour que cette différence soit due au hasard (on dit aussi due aux fluctuations d'échantillonnage).

On lit alors dans la table de la fonction de répartition de la loi de STUDENT, à la ligne n-1 et à la colonne 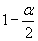le nombre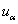

On peut alors conclure :

• Si t est dans l'intervalle ]-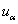;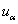[, alors on ne peut refuser H0 (il y a conformité).
• Si t n'est pas dans l'intervalle ]-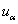;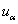[, que ce soit à droite ou à gauche, alors on refuse H0 au risque 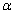(il n'y a pas conformité).