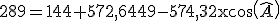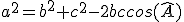Théorème des cosinus ( Th de Carnot)
 Le théorème
Le théorème
 |
Le théorème des cosinus s'écrit :
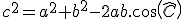
(il peut s'écrire aussi : 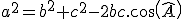 ou bien ou bien 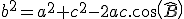 ) )
|
La démonstration n'est pas la même selon la forme du triangle.
Premier cas : le triangle est quelconque avec tous ses angles aigus (mesure < 90°).
 |
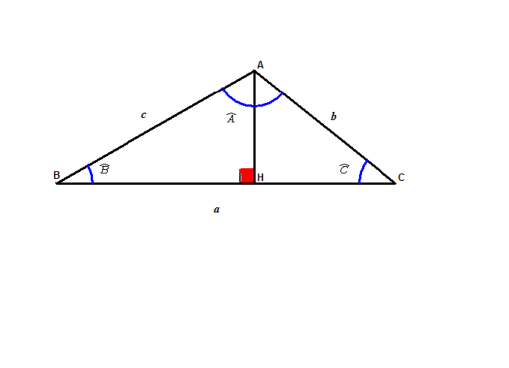
Dans le triangle rectangle BHA, on a AB2 = AH2 +BH2 (1)
Comme le triangle a tous ses angles aigus, le point H est entre B et C, donc BH = BC-HC et en remplaçant dans (1), on obtient :
AB2 = AH2 +(BC-HC)2 = AH2 + BC2 + HC2 -2 x BC x HC. (2)
Dans le triangle rectangle ACH, on obtient : AH2 = AC2 -CH2 et en remplaçant dans (2) :
AB2 = AC2 -CH2+ BC2 + HC2 -2 x BC x HC = AC2 + BC2 -2 x BC x HC.
On a d'autre part : 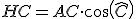 et au final : et au final :
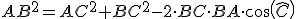
|
Deuxième cas : le triangle est quelconque avec un de ses angles obtus (mesure > 90°).
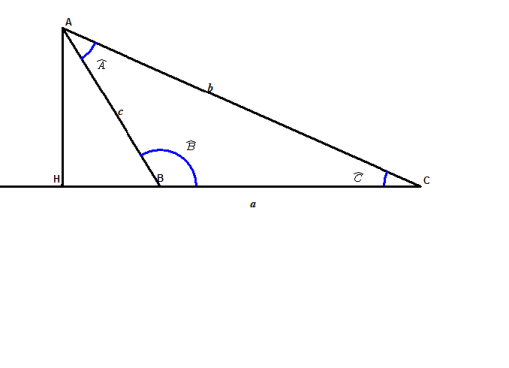 |
Dans le triangle rectangle BHA, on a AB2 = AH2 +BH2 (1)
Comme le triangle a un angle obtu, le point B est entre H et C, donc BH = HC-BC et en remplaçant dans (1), on obtient :
AB2 = AH2 +(HC-BC)2 = AH2 + BC2 + HC2 -2 x HC x BC. (2)
Dans le triangle rectangle ACH, on obtient : AH2 = AC2 -CH2 et en remplaçant dans (2) :
AB2 = AC2 -CH2+ BC2 + HC2 -2 x HC x BC = AC2 + BC2 -2 x HC x BC.
On a d'autre part : 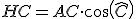 et au final : et au final :
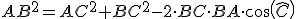
|
 Les cas d'utilisation du théorème des cosinus
Les cas d'utilisation du théorème des cosinus
On peut :
- calculer la longueur d'un côté connaissant les longueurs de deux côtés et la mesure d'un angle,
- Calculer la mesure d'un angle (et des deux autres) lorsque la longueur des trois côtés est connue.
 Exemple 1
Exemple 1
On donne un triangle quelconque ABC.
AC = 12, BC= 17, 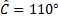 . On demande les autres caractéristiques du triangle, soit AB, et les deux autres angles.
. On demande les autres caractéristiques du triangle, soit AB, et les deux autres angles.
AC = b = 12 ; BC = a = 17. On souhaite calculer AB = c.
On utilise le théorème des cosinus, qui s'écrit ici : 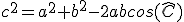 .
.
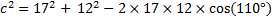
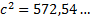
donc 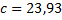 .
.
On peut maintenant calculer un des deux angles restants, soit avec le théorème des sinus, soit avec le théorème des cosinus.
Puisque il faut ici illustrer le théorème des cosinus, faisons le :
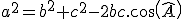 permet donc de calculer la mesure de l'angle
permet donc de calculer la mesure de l'angle 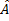
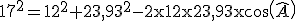 , d'où
, d'où 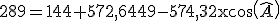
On obtient la valeur du cosinus de 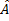 :
: 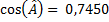 et enfin
et enfin 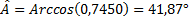 .
.
On en déduit la mesure de l'angle 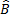 :
: 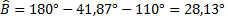 .
.
Tracez le triangle obtenu et vérifiez...
 Exemple 2
Exemple 2
On donne un triangle quelconque ABC.
AC = 10, BC= 14, AB = 18. On demande la mesure de l'angle 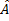 .
.
On utilise le théorème des cosinus : 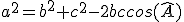
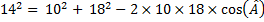 d'où
d'où 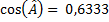
et enfin 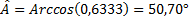
Tracez le triangle obtenu et vérifiez...

![]() . On demande les autres caractéristiques du triangle, soit AB, et les deux autres angles.
. On demande les autres caractéristiques du triangle, soit AB, et les deux autres angles.
![]() .
.
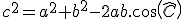
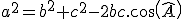 ou bien
ou bien 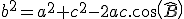 )
)
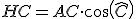 et au final :
et au final :
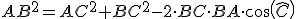

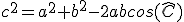 .
.
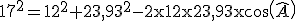 , d'où
, d'où