Dans le cas où 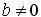 et
et 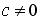 :
:
le nombre de racines du trinôme dépend du
signe du discriminant
Signe du
discriminant |
Racines factorisation
du trinôme |
Exemple |
|
Pas
de racines
et
pas
de factorisation |
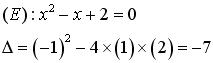
(E)
n’a pas de solution |
|
Une
racine (dite double) 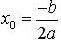
Factorisation
: 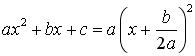 , ,
il s’agit
d’un produit remarquable |
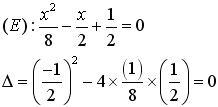
(E)
a une solution : 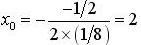
Factorisation : 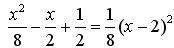
|
|
Deux
racines distinctes 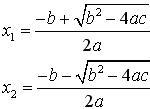
Factorisation
: 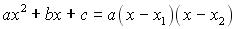
|
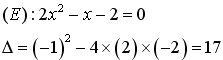
(E)
a deux solutions : 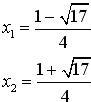
Factorisation
:
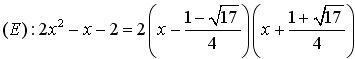
|

